机器人姿态（03）：坐标系和姿态

• 坐标系

无论是飞行器还是平衡车，都需要清楚机体自身的姿态。要了解姿态，首先需要知道地面坐标系和机体坐标系。

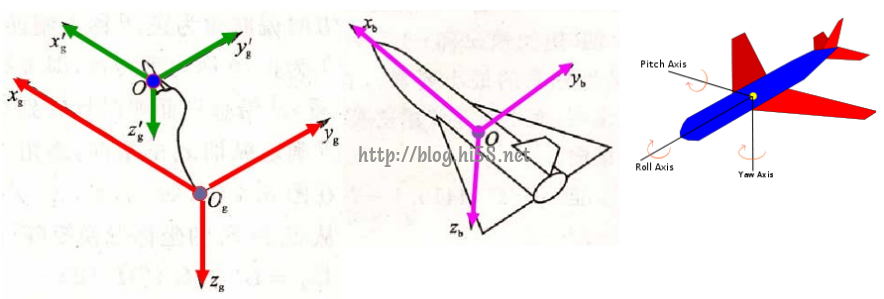
地面坐标系（earth-surface inertial reference frame），Sg=O_XgYgZg

在地面上选一点Og，使Xg轴在水平面内，并指向某一方向；Yg轴在水平面内，并垂直于Xg轴；Zg轴垂直于地面，并指向地心。

机体坐标系(aircraft body coordinate frame)，Sb=O_XbYbZb

原点O取在机体质心处，坐标系与机体固连；Xb轴在机体对称平面内，平行于机体设计轴线，而且指向机头；Yb轴垂直于飞机对称平面，指向机身右方；Zb轴在飞机对称平面内，与XY轴垂直并指向机身下方。

地面坐标系Sg和机体坐标系Sb的XYZ三个轴，其指向均由右手定则确定，即食指Ｘ／三小指Ｙ／拇指Ｚ，如下图：

• 姿态角（欧拉角）

姿态角，又叫欧拉角（Euler Angle），包括pitch/yaw/roll。这三个角度表示机体坐标系与地面坐标系的关系，可以反应机体相对于地面的姿态。（姿态角在机械行业也有借用，丝杆规格书中的pitch/yaw/roll就是表示类似概念的三个误差。）

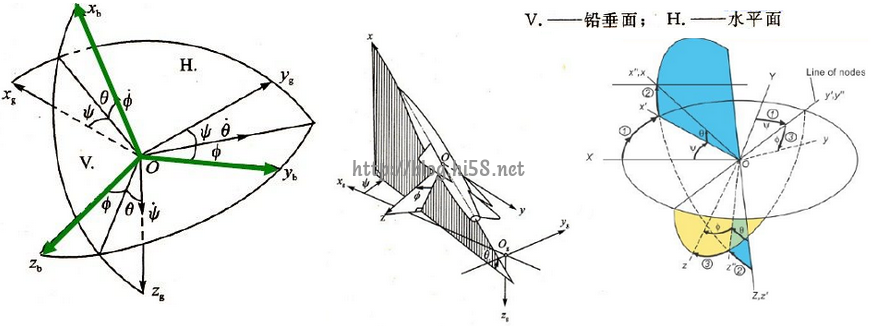
下面借用飞机的动画说明这三个角。

pitch，俯仰角，θ：是机体坐标系Xb轴与水平面的夹角；当Xb轴的正半轴位于过坐标原点的水平面之上（抬头）时，俯仰角为正，否则为负。

yaw，偏航角，ψ：是机体坐标系Xb轴在水平面上的投影与地面坐标系Xg轴之间的夹角，由Xg轴逆时针转至机体Xb的投影线时偏航角为正，即机头右偏航为正，反之为负。

roll，滚转角，Φ：是机体坐标系Zb轴与通过机体Xb轴的铅垂面间的夹角，即机体向右滚为正，反之为负。

航空领域把欧拉角叫作泰特-布莱恩特角（Tait-Bryan angle），由pitch（俯仰角）/roll（横滚角）/yaw（导航角）构成。它们在地朝下、在天朝上，选取东-北-天（E-N-U）地理坐标系为导航坐标系，称作n系，即以东面为X轴的正方向，北面为Y轴的正方向，天上（上面）为Z的正方向，如下图。

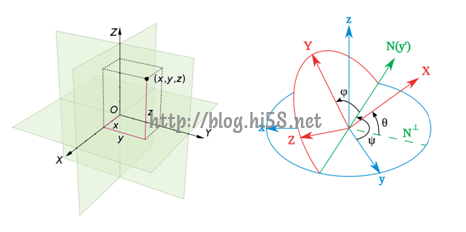
在上图中，Pitch、Yaw、Roll一般用表示，分别为绕Y轴、Z轴、X轴的旋转角度。

• 姿态矩阵

姿态角作为一种描述方位的方法，是用数学家Euler名字命名的，他首先证明了角位移序列等价于单个角位移，所以也叫欧拉角。欧拉角的基本思想是，将角位移分解为绕着三个正交轴的三个旋转角组成的序列。这对于习惯了笛卡儿坐标系的人们来说听着很复杂，其实是非常直观的，但更主要的是有用，因为欧拉角能用来描述任意旋转，用来构建姿态矩阵。

姿态矩阵（旋转矩阵）是3×3的矩阵，可以表示姿态。以工业机器人这样有级联旋转机构的设备为例，例如该机器人的手臂某时刻处于零姿态，其一级手臂末端点空间坐标为（X0，Y0，Z0），这是已知的。现在手臂旋转运动到了另一个姿态，此时一级手臂末端点空间坐标表示为（X1，Y1，Z1），那么如何求取现坐标（X1，Y1，Z1），这个时候就要用到姿态矩阵。 因为机械臂的旋转是由电机驱动的，电机旋转了多少角度可以通过编码器获知，那么就能找到这个时候手臂的欧拉角姿态，通过欧拉角就可以算出旋转矩阵，然后用（X0，Y0，Z0）的转置（3行1列向量）去乘以这个3×3矩阵，得到的3行1列向量就是（X1，Y1，Z1）。同理，手臂的第二级，第三级……，都可以照章办理。

• 四元数

四元数的定义是：

不经意看有点类似于机器视觉里面的齐次坐标，但四元数的内涵超出齐次坐标很多，有一些人在用四元数研究爱因斯坦的相对论。

对于视觉和运动中常见三种坐标变换：平移、缩放和旋转，旋转时最复杂。按照学习的习惯，人们更熟悉的是笛卡儿坐标的矩阵旋转和上面提到的欧拉旋转。矩阵旋转使用4*4的矩阵表示绕任意轴旋转的变换矩阵。欧拉旋转按照一定的坐标轴顺序绕每个轴轴旋转一定的角度来变换坐标向量。还有一种旋转的表示方法，就是四元数。

四元数又是什么？简单说四元数本质上是一种高阶复数，是一个四维空间。复数的二维空间在中学学过，一个复数由实部和虚部组成即x = a + bi，其中i是虚数单位，而且i^2 = -1。四元数其实与此类似，不同的是它的虚部包含了三个虚数单位i、j、k，即一个四元数由三个虚部组成x = a + bi + cj + dk。

那么四元数为什么又和三维旋转有关系呢？为了方便改写一下四元数x = ((x, y, z)，w) = (v, w)，其中v是向量，w是实数。

通过旋转轴和绕该轴旋转的角度，可以构造出四元数：

一般思路是思路： 6轴数据–>四元数–>欧拉角。