9. tf frame
抽象层面上,变换其实就是一种“偏移”(包括平移和旋转),代表了不同坐标系之间的变换和旋转。
在ROS中坐标系是3维的,用右手表示的,即食指X轴指向前方,其余四指Y轴指向左方,拇指Z轴指向上方。
许多ROS软件包都要使用TF软件功能包,以机器人识别的变换树的形式发布。
在tf中,两个坐标系的关系(也就是转换信息),用一个6自由度的相对位姿表示:
平移量(translation) + 旋转量(rotation)。类型分别是Vector3 和Quaternion 。
简单说tf类中定义了两个刚体之间的旋转与平移矩阵,并且重载了乘法运算符,这样就可以通过相乘两个tf来沿着tf树的方向求末段执行器相对世界坐标的位置与方向.
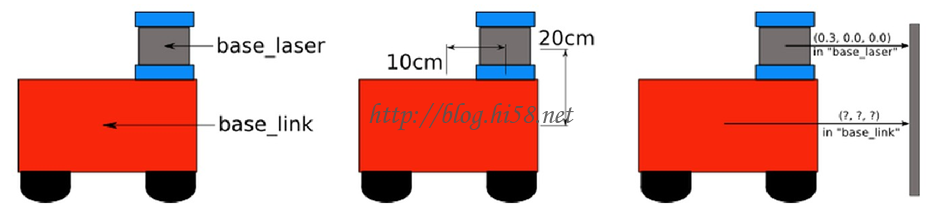
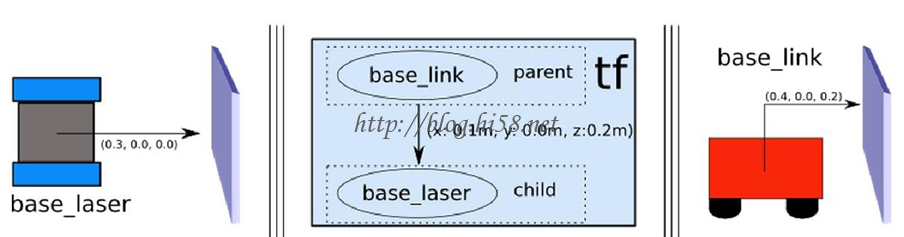
Let’s choose the “base_link” coordinat frame as the parent. This means the transform associated with the edge connecting “base_link” and “base_laser” should be (x: 0.1m, y: 0.0m, z: 0.2m).
For example beow shows that object in base-laser frame is (x: 0.3m, y: 0.0m, z: 0.0m) ,
例如:
and same object in base-link frame is (x: 0.4m, y: 0.0m, z: 0.2m).
9.1 TF软件包,最主要的是坐标转换的生产和消费。
TF基本原理是TransformBroadcaster(tb)生产信息,TransformListener(tl)消费信息。
所有的tb会发布某一特定的parent到child的变换,而所有tl会收到所有的这些变换,然后tl利用一个 tfbuffercore的数据结构维护一个完整的树结构及其状态。
因此,只要是一个tl,就要跟所有tb建立连接,就要收取所有的tf消息,来维护一颗完整的树并且搜索这棵树从而找到一条变换的路径,然后乘呀乘,每次都要如此。
广播树:
TF树结构的建立和维护是靠tf提供的tfbroadcastor的sendtransform接口。
tb发布一个从已有的parent frame到新的child frame的坐标系变换时,这棵树就会添加一个树枝,之后就是维护。
监听树:
用tf的tflisener监听某一个指定的从一个a frame到b frame的变换即可,当然前提是树上的树杈能把a,b联通。
这个变换是a frame->到b frame的变换,也表示了b frame在a frame的描述,也代表了一个在b frame里的点的坐标变换成在a frame里的坐标的坐标变换。
还是生产和消费好:
生产:
TransformBroadcaster有一个方法sendTransform发布坐标系1到坐标系2的旋转算子。
消费:
TransformListener有一个方法transformPoint用来变换坐标。
TransformListener有一个方法lookupTransform直接使用算子。
911. 生产
TransformBroadcaster有一个方法sendTransform发布坐标系1到坐标系2的旋转算子。
tf::TransformBroadcaster br;
tf::Quaternion q;//(x,y,z,w)
tf::Vector3 p; //(x,y,z)
tf::Transform ts; //(Quaternion(x,y,z,w), tf::Vector3(x,y,z))
tf::StampedTransform(ts, ros::Time::now(), “world”,”t1″)
那么这个这个发布:
br.sendTransform( tf::StampedTransform(ts, ros::Time::now(), “world”,”t1″) );
就是表明了t1坐标系在world坐标系的信息,评议是p:xyz适量所描述的那样,旋转是q:xyzw四元数所描述的那样。
也是说,word坐标系–>变换到t1坐标系的旋转算子就是【q,p】。
或者说,已知t1坐标系中的某点pont,其在world坐标系中的坐标就是【q,p】乘point。
再例如常见的,base_laser的激光安装在base_link的前方x=0.1m、左右正中心y=0、上方z=0.2m处的发布:
br.sendTransform( tf::TransformStamped ( tf::transform( tf::Quaternion(0,0,0,1), tf::Vector3(0.1,0,0.2), ros::time()::now(), “base_link”, “base_laser”) );
那么就是表明了base_laser激光坐标系base_link基坐标系的信息,平移是(0.1, 0.0, 0.2)适量所描述的那样, 旋转是(0,0,0,1)四元数所描述的那样。
也是说,base_link坐标系–>变换到base_laser坐标系的旋转算子就是【q,p】。
或者说,由base_laser激光坐标系扫描的数据点pont,其在base_link基坐标系中的坐标就是【q,p】乘point。
=== 例子 ===
某个机器人只有一个基本的移动机体,以及,挂在机体上方的激光。
这就定义了两个坐标系:一个对应于机体中心点的坐标系,一个对应于扫描仪中心的坐标系,分别取名为“base_link”和“baser_laser。
假设已经从传感器获取了一些数据,以一种代表了障碍物体到扫描仪中心点的距离的形式给出。
换句话说,已经有了一些“base_laser”坐标系的数据。
现在,期望通过这些数据,来帮助机器人避开物理世界的障碍物。
此处成功的关键是,需要一种方式,把传感器扫描的数据,从“base_laser”坐标系转换到“base_link”坐标系中去。
本质上,就是定义一种两个坐标系的关系。
为了定义这种关系,假设激光是挂在机体中心的前方10cm,高度20cm处,可以理解成传感器到机体中心的向量(0.1,0.0,0.2),这就等于给了一种转换的偏移关系。
具体来说,就是,从传感器到机体的坐标转换关系应该为(x:0.1m,y:0.0m, z:0.2m),相反的转换即是(x:-0.1m,y:0.0m,z:0.2m)。
基于该简单的例子的需求,需要创建两个frame,一个“base_link”,一个是“base_laser”。
为了定义两者的关系,首先需要决定谁是parent,谁是child。
时刻记得,由于tf假设所有的转换都是从parent到child的,因此谁是parent是有差别的。
这里选择“base_link”坐标系作为parent,其他的传感器等,都是被添加进robot的,对于“base_link”和“base_laser”他们来说,是最适合的。
这就意味着转换关系的表达式应该是(x:0.1m,y0.0m,z:0.2m)。
关系建立后,在收到“base_laser”的数据到“base_link”的转换过程,就可以是简单的调用tf库即可完成。
机器人就可以利用这些信息,在“base_link”坐标系中,就可以推理出传感器扫描出的数据,并可安全的规划路径和避障等工作。
以上层来描述“base_laser”坐标系的点,来转换到”base_link”坐标系。
9.2 相应代码
921. 生产
TransformBroadcaster有一个方法sendTransform发布坐标系1到坐标系2的旋转算子。
922 消费方法一
TransformListener有一个方法transformPoint用来变换坐标。
923 消费方法二
TransformListener有一个方法lookupTransform直接使用算子。
921. 生产
TransformBroadcaster有一个方法sendTransform发布坐标系1到坐标系2的旋转算子。
ros::NodeHandle n;
ros::Rate r(100);
tf::TransformBroadcaster br;
//create a TransformBroadcaster object to send base_link → base_laser transform
while(n.ok()){
br.sendTransform( tf::TransformStamped ( tf::transform( tf::Quaternion(0,0,0,1), tf::Vector3(0.1,0,0.2), ros::time()::now(), “base_link”, “base_laser”) );
r.sleep();
}
HINTS:
broadcaster.sendTransform() Sending a transform with a TransformBroadcaster requires five arguments need 4 params:
PARAM1 = tf::StampedTransform( PARAM1=tf::Transform(tf::Quaternion(0, 0, 0, 1), tf::Vector3(0.1, 0.0, 0.2)),
PARAM2=ros::Time::now(),
PARAM3=”base_link”,
PARAM4=”base_laser”
PARAM1:
First, we pass in the rotation transform, which is specified by a btQuaternion for any rotation that needs to occur between the two coordinate frames.
In this case, we want to apply no rotation, so we send in a btQuaternion constructed from pitch, roll, and yaw values equal to zero.
Second, a btVector3 for any translation that we’d like to apply. We do, however, want to apply a translation, so we create a btVector3 corresponding to the laser’s x offset of 10cm and z offset of 20cm from the robot base.
And, we need to give the transform being published a timestamp, we’ll just stamp it with ros::Time::now().
And, We need to pass the name of the parent node of the link we’re creating, in this case “base_link.”
And, we need to pass the name of the child node of the link we’re creating, in this case “base_laser.”
922 消费方法一
TransformListener有一个方法transformPoint用来变换坐标。
这是建立了一个定时器,定时把base_laser坐标系的数据转换到base-link坐标系里使用。
#include <tf/transform_listener.h>
// 作用: 将“base_laser”坐标系的点,变换到“base_link”坐标系中。
ros::NodeHandle n;
tf::TransformListener listener(ros::Duration(10));
//transform a point once every second
ros::Timer timer = n.createTimer(ros::Duration(1.0), boost::bind(&transformPoint, boost::ref(listener)));
ros::spin();
//这个函数将会以ros::Timer定义的周期,作为一个回调函数周期调用。目前周期是1s
void transformPoint(const tf::TransformListener& listener)
//创建一个虚拟点,作为geometry_msgs::PointStamped。
//消息名字最后的”Stamped”的意义是,它包含了一个头部,允许我们去把时间戳和消息的frame_id相关关联起来。
geometry_msgs::PointStamped laser_point;
//关联frame_id也就是将node定义为frame_id
laser_point.header.frame_id = “base_laser”;
//设置laser_point的时间戳为ros::time(),即是允许我们请求TransformListener取得最新的变换数据
laser_point.header.stamp = ros::Time();
//伪造几个虚拟的点,即所需要变换过去的数据
laser_point.point.x = 1.1;
laser_point.point.y = 2.2;
laser_point.point.z = 3.3;
geometry_msgs::PointStamped base_point;
//通过TransformListener对象,调用transformPoint(),填充三个参数来进行数据变换
listener.transformPoint(“base_link”, laser_point, base_point);
//arg1,代表想要变换到的目标坐标系的名字。
//arg2,填充需要变换的原始坐标系的点对象。
//arg3,目标坐标系的点对象。
… …
ROS_INFO(“base_laser: (%.2f, %.2f. %.2f) —–> base_link: (%.2f, %.2f, %.2f) at time %.2f”,
laser_point.point.x, laser_point.point.y, laser_point.point.z,
base_point.point.x, base_point.point.y, base_point.point.z, base_point.header.stamp.toSec());
//THEN base_point should be (1.1, 2, 3.2).
923 消费方法二
TransformListener有一个方法lookupTransform直接使用算子。
ros::Publisher base_laser_vel = node.advertise(“base_laser/cmd_vel”, 10); // to control
tf::TransformListener listener;
ros::Rate rate(10.0);
while (node.ok()){
try {
listener.waitForTransform(“/base_link”, “/base_laser”, ros::Time(0), ros::Duration(10.0) );
listener.lookupTransform(“/base_link”, “/base_laser”, ros::Time(0), transform );
} catch (tf::TransformException &ex) {
ROS_ERROR(“%s”,ex.what());
}
geometry_msgs::Twist vel_msg;
vel_msg.angular.z = 4.0 * atan2(transform.getOrigin().y(),transform.getOrigin().x());
vel_msg.linear.x = 0.5 * sqrt(pow(transform.getOrigin().x(), 2) + pow(transform.getOrigin().y(), 2));
base_laser_vel.publish(vel_msg);
//while transform of t2 in t1 is iavailable then cal new linear and angular data for turtle2
//based on its distance and angle from turtle1
//New velocity is published in the topic “turtle2/cmd_vel”, t2 = base_laser
//HINTS: turtle2 is the dest child we needed, tutlr1 is the source parent we based.
rate.sleep();
}
这个是一旦等到”/base_link”, “/base_laser的变换可用,就取出这个transform,根据base_laser的数据信息控制base_link行为。
9.3. 发布变换的几种方式
931 常见方式的代码:
#include<tf/transform_broadcaster.h>
void posecallback(turtlesim::PoseConstPtr &msg)
static tf::TransformBroadcaster br;
//创建Transform存储变换相关信息,它包含旋转和位移的信息,有一个向量Vector3表示坐标,以及四元组表示方向。
tf::Transform transform;
//创建四元组
tf::Quaternion q;
//调用q的方法,绕着z轴旋转,有下面参数形式
q.setRPY(0,0,msg->theta);
//填充transform
transform.setOrigin(tf::Vector3(msg->x,msg->y,0));
transform.setRotation(q);
//创建一个transform::stamped对象,广播出去
br.sendTransform(tf::StampedTransform(transform,ros::Time::now(),”world”,”turtle1″));
…
}
解释直接在代码了。
932 其实变换可以直接用四元数:
transform.setOrigin( tf::Vector3(0.0, 0.0, 0.0) );
transform.setRotation( tf::Quaternion(0, 0, 0, 1) );
br.sendTransform(tf::StampedTransform(transform,ros::Time::now(), “world”, “turtle1″)
这三句话分别做了以下工作:
设置turtle1在world坐标系下的坐标原点
设置turtle1相对于world的旋转角度,这里用四元数表示
发送变换信息
933 上面这种四元数表示旋转角度的方式不太直观,写代码的时候一般不想将旋转变换换算成四元数,
大部分采用前面代码中的下方法写这个变换:
tf::Quaternion q;
q.setRPY(0, 0, msg->theta);
transform.setOrigin( tf::Vector3(msg->x, msg->y, 0.0) );
transform.setRotation(q);
br.sendTransform(tf::StampedTransform(transform,ros::Time::now(),”world”,”turtle1″));
这三句话,直接用RPY(分别对应绕XYZ轴旋转角度)来设置旋转变换了
934 还有一种使用静态变换:
static_transform_publisher工具的功能是发布两个参考系之间的静态坐标变换,两个参考系一般不发生相对位置变化。
static_transform_publisher x y z yaw pitch roll frame_id child_frame_id period_in_ms
static_transform_publisher x y z qx qy qz qw frame_id child_frame_id period_in_ms
以上两种命令格式,需要设置坐标的偏移和旋转参数。
偏移参数都使用相对于xyz三轴的坐标位移。
而旋转参数,第一种命令格式使用以弧度为单位的 yaw/pitch/roll三个角度,第二种命令格式使用四元数表达旋转角度。
发布频率以ms为单位,一般100ms比较合适。
Publish a static coordinate transform to tf using an x/y/z offset in meters and yaw/pitch/roll in radians. (yaw is rotation about Z, pitch is rotation about Y, and roll is rotation about X). The period, in milliseconds, specifies how often to send a transform. 100ms (10hz) is a good value.
935 br.sendTransform(tf::StampedTransform(transform,ros::Time::now(), “world”, “turtle1”)
这种发布都是完成一个工作, 表明t1坐标系相对于world坐标系的位置关系,是旋转角度或四元数所描述的那样。
这样,如果t1坐标系里面有激光或里程计发布数据, 位于world和t1坐标系之外的其他坐标系,即可获得任何可能的坐标系下面的激光或历程数据。