神经网络三种

—— PART I —— 深度神经网络 DNN
1. DNN 模型
1.1 从感知机到神经网络
1.3 DNN基本结构
1.5 DNN前向传播
3 梯度下降 – Gradient Descent
3.1 梯度
3.3 梯度下降解释
3.5 相关概念
3.7 详细算法
3.9 算法优化
5. DNN 反向传播
5.1 基本思路
5.2 算法过程
7. 损失函数和激活函数
7.1 均方差+Sigmoid的组合
7.3 交叉熵损失函数+Sigmoid激活函数
7.5 对数似然损失函数和softmax激活函数
7.7 其他激活函数
7.9 梯度爆炸梯度消失
—— PART II —— 卷积神经网络 CNN
1. 卷积
3. CNN的结构
5. 卷积层
7. 池化层
9. CNN的前向传播
9.1 输入层前向传播到卷积层
9.3 隐藏层前向传播到卷积层
9.5 隐藏层前向传播到池化层
9.7 隐藏层前向传播到全连接层
9.9 小结
11. CNN的反向传播
11.1 算法思想
11.3 推导上一隐藏层
11.5 推导上一隐藏层
11.7 推导该层的W,b梯度
11.9 总结
—— PART II —— 循环神经网络 RNN
1. CNN 结构
3. 前向传播算法
5. 反向传播算法

—— PART I —— 深度神经网络 DNN

深度神经网络（Deep Neural Networks）是深度学习的基础，要理解DNN，首先要理解DNN模型。

1. DNN 模型

1.1 从感知机到神经网络

感知机，是一个有若干输入和一个输出的模型：

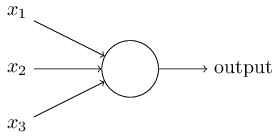
输出和输入之间学习到一个线性关系，得到中间输出结果：
z=∑i（wixi+b）

接着是一个神经元激活函数:
sign(z)={−1 or 1}
从而得到想要的输出结果1或者-1。

这个模型只能用于二元分类，且无法学习比较复杂的非线性模型，因此在工业界无法使用。

神经网络则在感知机的模型上做了扩展，总结下主要有三点：
1）加入了隐藏层，隐藏层可以有多层，增强模型的表达能力。
2）输出层的神经元也可以不止一个输出，可以有多个输出，这样模型可以灵活的应用于分类回归，以及其他的机器学习领域比如降维和聚类等。
3） 对激活函数做扩展，感知机的激活函数是sign(z)sign(z),虽然简单但是处理能力有限，因此神经网络中一般使用的其他的激活函数，比如在逻辑回归里面使用的Sigmoid函数f(z) = 1 /（1 + exp(−z)）。还有后来出现的tanx, softmax,和ReLU等。使用不同的激活函数，神经网络的表达能力进一步增强。

1.3 DNN基本结构

神经网络是基于感知机的扩展，而DNN可以理解为有很多隐藏层的神经网络。所以DNN有时也叫做多层感知机（Multi-Layer perceptron,MLP）。
从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层。一般来说第一层是输出层，最后一层是输出层，而中间的层数都是隐藏层。

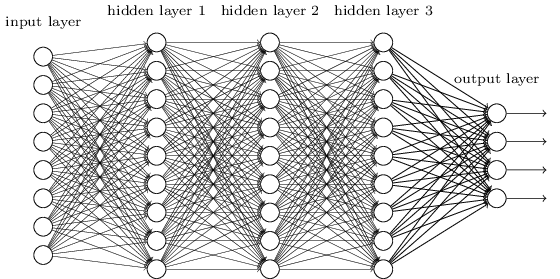
层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。
所以虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系z=∑（wixi+bz）加上一个激活函数σ(z)。

由于DNN层数多，线性关系系数w和偏倚b的数量也就是很多了。

a） 首先看线性关系系数w的定义

以下图一个三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的线性系数定义为w3_24。
上标3代表线性系数ww所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。

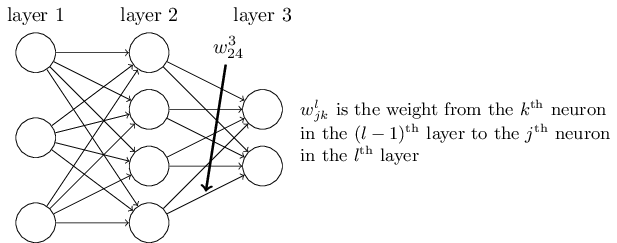
为什么不是w3_42, 而是w3_24呢？这主要是为了便于模型用于矩阵表示运算，如果是w3_24而每次进行矩阵运算是wTx+b，需要进行转置。将输出的索引放在前面的话，则线性运算不用转置,即直接为wx+bwx+b。
总结下，第l−1层的第k个神经元到第l层的第j个神经元的线性系数定义为wl_jk。
注意，输入层是没有w参数的。

b） 再看偏倚b的定义

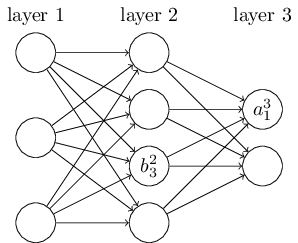
还是以这个三层的DNN为例，第二层的第三个神经元对应的偏倚定义为b2_3。
其中，上标2代表所在的层数，下标3代表偏倚所在的神经元的索引。
同样的道理，第三个的第一个神经元的偏倚应该表示为b3_1。
同样的，输入层是没有偏倚参数b的。

1.5 DNN前向传播

对于下图的三层DNN：

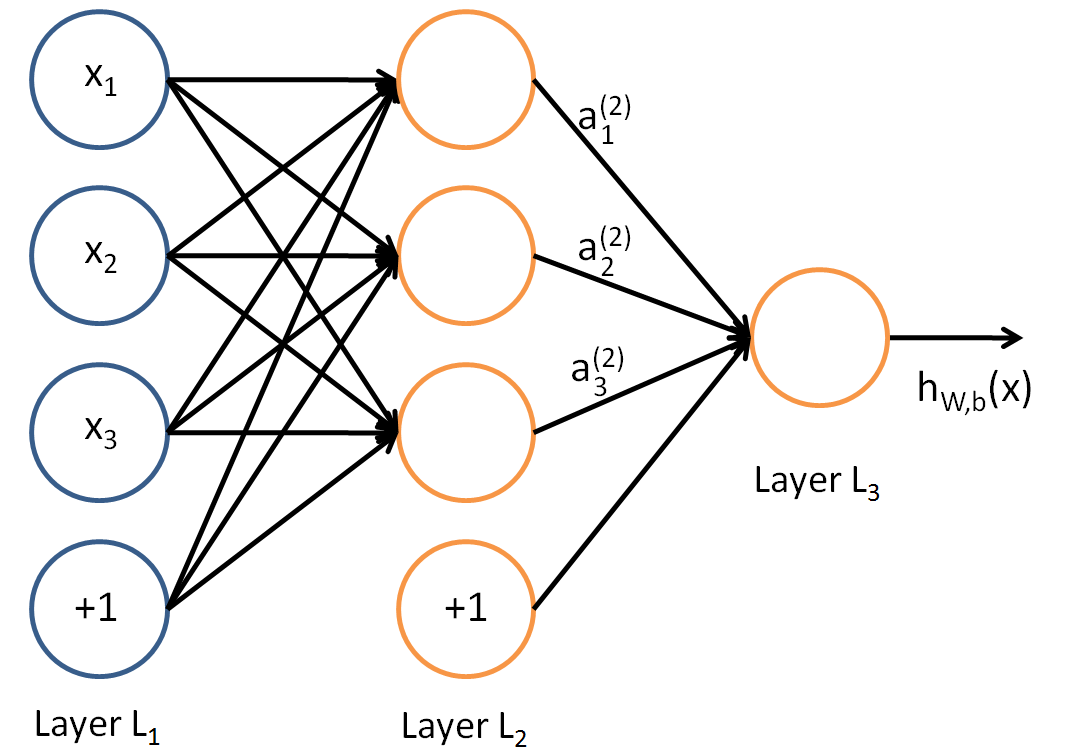
假设选择的激活函数是σ(z)，隐藏层和输出层的输出值为a，则利用和感知机一样的思路，可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。
对于第二层的的输出a21,a22,，有：
对于第三层的的输出a31，有：

所谓的DNN的前向传播算法也就是利用若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。
输入: 总层数L，所有隐藏层和输出层对应的矩阵W,偏倚向量b，输入值向量x
输出：输出层的输出a

过程：
1） 初始化a1=x
2) for l=2 to L, 计算：al=σ(zl)=σ(W_la_l−1+bl)

怎么得到最优的矩阵W,偏倚向量b？需要DNN的反向传播算法。
REF ： http://www.cnblogs.com/pinard/p/6418668.html

3 梯度下降 – Gradient Descent

在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的是最小二乘法。

3.1 梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。
比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)T,以此类推。

梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。
具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。
或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x0, ∂f/∂y0)T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。
反过来，如果需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

梯度下降法和梯度上升法是可以互相转化的。比如需要求解损失函数f(θ)的最小值，这时需要用梯度下降法来迭代求解。但是实际上，可以反过来求解损失函数 -f(θ)的最大值，这时梯度上升法就派上用场了。
下面详细说梯度下降法。

3.3 梯度下降解释

首先来看看梯度下降的一个直观的解释。
比如我们在一座大山上的某处位置，由于不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。
这样一步步的走下去，一直走到觉得已经到了山脚。当然这样走下去，有可能不能走到山脚，而是到了某一个局部的山峰低处。
从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。
当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

3.5 相关概念

* 步长（Learning rate）
步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。
下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

* 特征（feature）
指的是样本中输入部分，比如样本（x0,y0）,（x1,y1）,则样本特征为x，样本输出为y。

* 假设函数（hypothesis function）
在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)。
比如对于样本（xi,yi）(i=1,2,…n),可以采用拟合函数如下： hθ(x) = θ0+θ1x。

* 损失函数（loss function）
为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。
损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。
在线性回归中，损失函数通常为样本输出和假设函数的差取平方。

3.7 详细算法

梯度下降法的算法可以有代数法和矩阵法（也称向量法）两种表示。
矩阵法更加的简洁，且由于使用了矩阵，实现逻辑更加的一目了然。

a） 代数方式
b） 矩阵方式

3.9 算法优化

哪些地方需要调优？
1. 算法的步长选择。
2. 算法参数的初始值选择。
3.归一化。

5. DNN 反向传播

DNN反向传播算法要解决的问题，也就是说，什么时候需要这个反向传播算法.回到监督学习的一般问题：
有m个训练样本：{(x1,y1),(x2,y2),…,(xm,ym），其中x为输入向量，特征维度为n_in,而y为输出向量，特征维度为n_out。
需要利用这m个样本训练出一个模型，当有一个新的测试样本(xtest,?)来到时, 可以预测ytest向量的输出。

如果采用DNN的模型，即使输入层有n_in个神经元，而输出层有n_out个神经元。再加上一些含有若干神经元的隐藏层。
此时需要找到合适的所有隐藏层和输出层对应的线性系数矩阵W,偏倚向量b,让所有的训练样本输入计算出的输出尽可能的等于或很接近样本输出。怎么找到合适的参数呢？

如果对传统的机器学习的算法优化过程熟悉的话，就很容易联想到可以用一个合适的损失函数来度量训练样本的输出损失，接着对这个损失函数进行优化求最小化的极值，对应的一系列线性系数矩阵W,偏倚向量b即为最终结果。

在DNN中，损失函数优化极值求解的过程最常见的一般是通过梯度下降法来一步步迭代完成的，当然也可以是其他的迭代方法比如牛顿法与拟牛顿法。

5.1 基本思路

在进行DNN反向传播算法前，需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。
训练样本计算出的输出是怎么得来的？这 个输出是随机选择一系列W,b, 通过前向传播算法计算出来的。

DNN可选择的损失函数有不少，为了专注算法，这里使用最常见的均方差来度量损失。
J(W,b,x,y)=12||aL−y||22， 这个||S||2为S的L2范数。

损失函数有了，现在开始用梯度下降法迭代求解每一层的W,b。
首先是输出层第LL层。注意到输出层的W,b满足下式：
aL=σ(zL)=σ(WLaL−1+bL)
对于输出层的参数，损失函数变为：
J(W,b,x,y)=12||aL−y||22=12||σ(WLaL−1+bL)−y||22
这样求解W,bW,b的梯度就简单了：
–
注意到在求解输出层的W,bW,b的时候，有公共的部分∂J(W,b,x,)/∂zL，可以把公共的部分即对zLzL先算出来，记为：
δL=∂J(W,b,x,y)/∂zL
这样终于把输出层的梯度算出来了。
那么如何计算上一层L−1层的梯度，上上层L−2层的梯度呢？需要一步步的递推，注意到对于第l层的未激活输出zl，它的梯度可以表示为:
δl=∂J(W,b,x,y)/∂zl
可以依次计算出第ll层的δlδl,则该层的Wl,blWl,bl很容易计算。为什么呢？注意到前向传播算法，有：
zl=Wlal−1+bl
这样得到了δl的递推关系式。只要求出了某一层的δl，求解Wl,bl的对应梯度就很简单的。

5.2 算法过程

总结下DNN反向传播算法的过程。
由于梯度下降法有批量（Batch），小批量(mini-Batch)，随机三个变种，为了简化描述，这里以最基本的批量梯度下降法为例来描述反向传播算法。
实际上在业界使用最多的是mini-Batch的梯度下降法。不过区别仅仅在于迭代时训练样本的选择而已。

输入: 总层数L，以及各隐藏层与输出层的神经元个数，激活函数，损失函数，迭代步长α,最大迭代次数MAX与停止迭代阈值ϵ，输入的m个训练样本{(x1,y1),(x2,y2),…,(xm,ym)}
输出：各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b

过程：
1) 初始化各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b的值为一个随机值。
2）for iter to 1 to MAX：
2-1) for i =1 to m：
a) 将DNN输入a1a1设置为xi
b) for ll=2 to L，进行前向传播算法计算 ai,l
c) 通过损失函数计算输出层的δi,L
d) for ll= L to 2, 进行反向传播算法计算 δi,l
2-2) for ll = 2 to L，更新第ll层的Wl,blWl,bl:
2-3) 如果所有W，bW，b的变化值都小于停止迭代阈值ϵϵ，则跳出迭代循环到步骤3。
3） 输出各隐藏层与输出层的线性关系系数矩阵WW和偏倚向量bb。

7. 损失函数和激活函数

前面使用的损失函数是均方差，而激活函数是Sigmoid。实际上DNN可以使用的损失函数和激活函数不少。

7.1 均方差+Sigmoid的组合

从图可以看出，对于Sigmoid，当z的取值越来越大后，函数曲线变得越来越平缓，意味着此时的导数σ′(z)也越来越小。同样的，当z的取值越来越小时，也有这个问题。

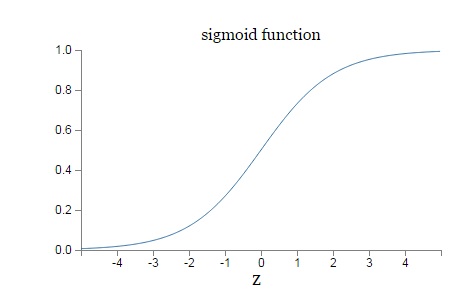
Sigmoid的这个曲线意味着在大多数时候，梯度变化值很小，导致W,b更新到极值的速度较慢，也就是算法收敛速度较慢。

7.3 交叉熵损失函数+Sigmoid激活函数

如何改进呢？换掉Sigmoid？这当然是一种选择。
另一种常见的选择是用交叉熵损失函数来代替均方差损失函数。

样本的交叉熵损失函数的形式：
J(W,b,a,y)=−y∙lna − (1−y)∙ln(1−a)
其中，∙∙为向量内积。
这个损失函数的学名叫交叉熵。

当使用交叉熵时，各层δl的梯度梯度表达式里面已经没有了σ′(z)，梯度为预测值和真实值的差距，因此避免了反向传播收敛速度慢的问题。

7.5 对数似然损失函数和softmax激活函数

前面都假设输出是连续可导的值。
但是如果是分类问题，那么输出是一个个的类别，那怎么用DNN来解决这个问题呢？
比如假设有一个三个类别的分类问题，这样DNN输出层应该有三个神经元，假设第一个神经元对应类别一，第二个对应类别二，第三个对应类别三，这样期望的输出应该是(1,0,0)，（0,1,0）和(0,0,1)这三种。即样本真实类别对应的神经元输出应该无限接近或者等于1，而非改样本真实输出对应的神经元的输出应该无限接近或者等于0。或者说，希望输出层的神经元对应的输出是若干个概率值，这若干个概率值即DNN模型对于输入值对于各类别的输出预测，同时为满足概率模型，这若干个概率值之和应该等于1。

DNN分类模型要求是输出层神经元输出的值在0到1之间，同时所有输出值之和为1。很明显，现有的普通DNN是无法满足这个要求的。但只需要对现有的全连接DNN稍作改良，即可用于解决分类问题。在现有的DNN模型中，可以将输出层第i个神经元的激活函数定义为如下形式：
aLi=ezLi∑j=1nLezLj
其中，nL是输出层第L层的神经元个数，或者说分类问题的类别数。
很容易看出，所有的aLi都是在(0,1) 之间的数字。

这个方法很简洁，仅仅只需要将输出层的激活函数从Sigmoid之类的函数转变为上式的激活函数即可。
上式这个激活函数就是softmax激活函数。它在分类问题中有广泛的应用。
将DNN用于分类问题，在输出层用softmax激活函数也是最常见的了。

下面这个例子清晰的描述了softmax激活函数在前向传播算法时的使用。假设输出层为三个神经元，而未激活的输出为3,1和-3，求出各自的指数表达式为：20,2.7和0.05，归一化因子即为22.75，这样就求出了三个类别的概率输出分布为0.88，0.12和0。

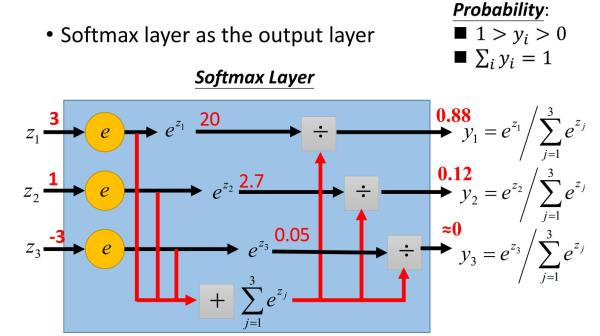
7.7 其他激活函数

tanh：这个是sigmoid的变种，表达式为：
tanh(z)=ez−e−z / ez+e−z

7.9 梯度爆炸梯度消失

什么是梯度爆炸和梯度消失呢，就是在反向传播的算法过程中，由于使用了是矩阵求导的链式法则，有一大串连乘，如果连乘的数字在每层都是小于1的，则梯度越往前乘越小，导致梯度消失，而如果连乘的数字在每层都是大于1的，则梯度越往前乘越大，导致梯度爆炸。

一个可能部分解决梯度消失问题的办法是使用ReLU（Rectified Linear Unit）激活函数，ReLU在卷积神经网络CNN中得到了广泛的应用.

—— PART II —— 卷积神经网络 CNN

在DNN大类中，卷积神经网络(Convolutional Neural Networks，以下简称CNN)是最为成功的DNN特例之一。

1. 卷积

微积分中卷积表达为：S(t)=∫x(t−a)w(a)da，
离散形式是：s(t)=∑（x(t−a)w(a)）
用矩阵表示可以为：s(t)=(X∗W)(t)， 其中星号表示卷积。
如果是二维的卷积，则表示式为：s(i,j)=(X∗W)(i,j)=∑m∑n 【x(i−m,j−n)w(m,n)】
CNN中对于二维的卷积，定义为：s(i,j)=(X∗W)(i,j)=∑m∑n【x(i+m,j+n)w(m,n)】，并不是严格意义上的卷积。其中，X为输入，W为卷积核。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵。但是如果X是多维张量，那么W也是一个多维的张量。

3. CNN的结构

一个常见的CNN例子：

图中是一个图形识别的CNN模型。
最左边的船的图像就是输入层，计算机理解为输入若干个矩阵，这点和DNN基本相同。
接着是卷积层，CNN特有的。卷积层的激活函数使用的是ReLU。它其实很简单，就是ReLU(x)=max(0,x)。
在卷积层后面是池化层，也是CNN特有的。池化层没有激活函数。
卷积层+池化层的组合可以在隐藏层出现很多次，上图中出现两次。实际上这个次数是根据模型的需要而来的。也可以灵活使用使用卷积层+卷积层，或者卷积层+卷积层+池化层的组合，这些在构建模型的时候没有限制。但是最常见的CNN都是若干卷积层+池化层的组合，如上图中的CNN结构。
在若干卷积层+池化层后面是全连接层，就是前面的DNN结构，只是输出层使用了Softmax激活函数来做图像识别的分类。

可以看出，CNN相对于DNN，比较特殊的是卷积层和池化层。

5. 卷积层

CNN中的卷积，假如是对图像卷积，其实就是对输出的图像的不同局部的矩阵和卷积核矩阵各个位置的元素相乘，然后相加得到。
举个例子如下，图中的输入是一个二维的3×4的矩阵，而卷积核是一个2×2的矩阵。

假设卷积是一次移动一个像素来卷积的，那么：
首先对输入的左上角2×2局部和卷积核卷积，即各个位置的元素相乘再相加，得到的输出矩阵S的S00S00的元素，值为aw+bx+ey+fzaw+bx+ey+fz。
接着将输入的局部向右平移一个像素，现在是(b,c,f,g)四个元素构成的矩阵和卷积核来卷积，这样得到了输出矩阵S的S01的元素。
同样的方法，可以得到输出矩阵S的S02，S10，S11，S12的元素。
最终得到卷积输出的矩阵为一个2×3的矩阵S。

再举一个动态的卷积过程的例子：
这个绿色的5×5输入矩阵，卷积核是一个下面这个黄色的3×3的矩阵，卷积的步幅是一个像素。
则卷积的过程如下面的动图。卷积的结果是一个3×3的矩阵。

上面2个例子都是二维的输入，卷积的过程比较简单，那么如果输入是多维的呢？
例如在前面一组卷积层+池化层的输出是3个矩阵，这3个矩阵作为输入呢，那么怎么去卷积呢？
又比如输入的是对应RGB的彩色图像，即是三个分布对应R，G和B的矩阵呢？
SEE ： http://cs231n.github.io/assets/conv-demo/index.html

7. 池化层

相比卷积层的复杂，池化层则要简单的多，所谓的池化，就是对输入张量的各个子矩阵进行压缩。
假如是2×2的池化，那么就将子矩阵的每2×2个元素变成一个元素，如果是3×3的池化，那么就将子矩阵的每3×3个元素变成一个元素，这样输入矩阵的维度就变小了。
要想将输入子矩阵的每nxn个元素变成一个元素，那么需要一个池化标准。常见的池化标准有2个，MAX或者是Average。即取对应区域的最大值或者平均值作为池化后的元素值。

9. CNN的前向传播

CNN的结构，包括输出层，若干的卷积层+ReLU激活函数，若干的池化层，DNN全连接层，以及最后的用Softmax激活函数的输出层。
用一个彩色的汽车样本的图像识别再从感官上回顾下CNN的结构。图中的CONV即为卷积层，POOL即为池化层，而FC即为DNN全连接层，包括了最后的用Softmax激活函数的输出层。

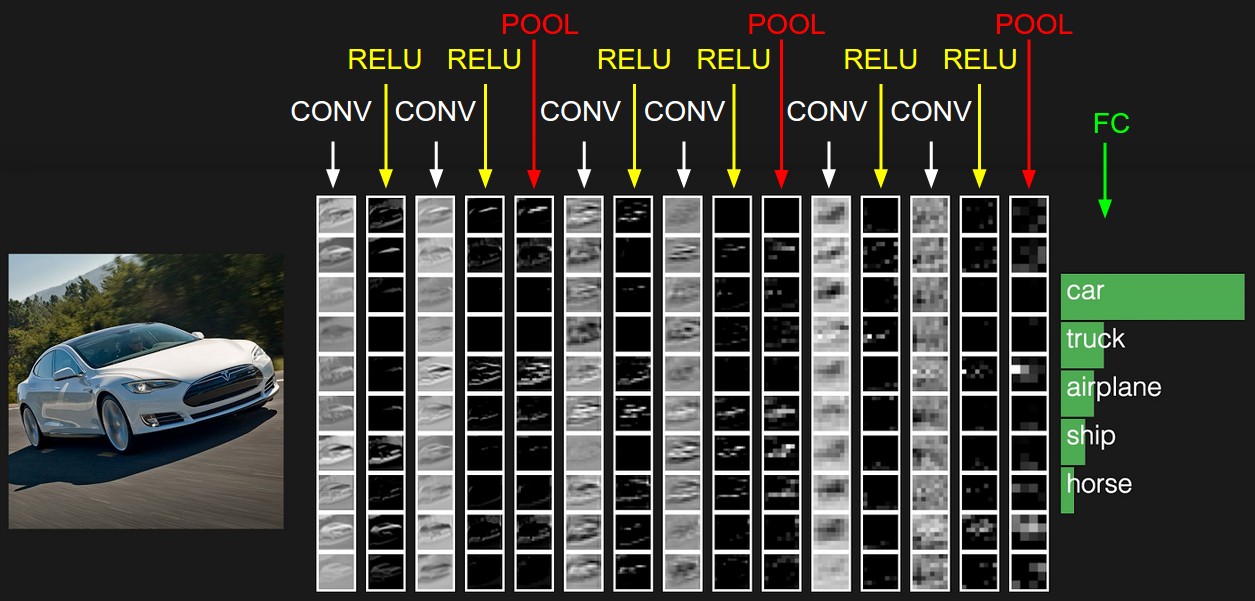
要理顺CNN的前向传播算法，重点是输入层的前向传播，卷积层的前向传播以及池化层的前向传播。

9.1 输入层前向传播到卷积层
9.3 隐藏层前向传播到卷积层
9.5 隐藏层前向传播到池化层
9.7 隐藏层前向传播到全连接层
9.9 小结

11. CNN的反向传播

DNN同样的思想可以用到CNN中，不过很明显，CNN有些不同的地方，不能直接去套用DNN的反向传播算法的公式。

11.1 算法思想
11.3 推导上一隐藏层
11.5 推导上一隐藏层
11.7 推导该层的W,b梯度
11.9 总结

—— PART II —— 循环神经网络 RNN

DNN以及DNN的特例CNN，这些算法都是前向反馈的，模型的输出和模型本身没有关联关系，输出和模型间有反馈的神经网络的就是RNN。
在DNN和CNN中，训练样本的输入和输出是比较的确定的。但是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。
而对于这类问题，RNN则比较的擅长。例如字符级语言模型的RNN，它依然是一个神经网络，其基本结构与普通的神经网络基本一致的：

那么RNN是怎么做到的呢？
RNN假设样本是基于序列的。比如是从序列索引1到序列索引t的。
对于这其中的任意序列索引号t,它对应的输入是对应的样本序列中的x(t)。
而模型在序列索引号t位置的隐藏状态h(t)，则由x(t)和在t−1位置的隐藏状态h(t−1)共同决定。
在任意序列索引号t，也有对应的模型预测输出o(t)。
通过预测输出o(t)和训练序列真实输出y(t),以及损失函数L(t)，就可以用DNN类似的方法来训练模型，接着用来预测测试序列中的一些位置的输出。

因此，不同之处是，传统的神经网络（包括CNN）假定所有输入和输出都是相互独立的，而RNN的基本假设是输入序列之间是存在相互影响的。
RNN之所以被称为循环，就是它会按照序列的输入时间不断重复训练该网络，并利用后向传播算法不断迭代更新权重(U,V,W， 这也就是为什么可以将RNN一层网络“展开”为n层，而n是序列输入的长度，也是时间总步长。
同时的，也不难理解为什么一个RNN层“展开”的结点都共用一套参数。这里的“展开”是虚拟的。

1. CNN 结构
来看看RNN的模型：

左边是RNN模型没有按时间展开的图，按时间序列展开，则是上图中的右边部分。
重点观察右边，图描述了在序列索引号t附近RNN的模型

RNN 参数：
U是从输入层到隐藏层的参数，V是隐藏层到输出层的参数，W是t时刻到t+1时刻的参数。

RNN 基本算法：
* xt是t时刻的输入，代表在序列索引号t时训练样本的输入。可以是单词， 或者句子的One-hot编码。同样的，x(t−1)和x(t+1)代表t−1和t+1时训练样本的输入。
* h(t)， 代表在序列索引号t时模型的隐藏状态。h(t)由x(t)和h(t−1)共同决定。
* o(t)代表在序列索引号t时模型的输出。o(t)只由模型当前的隐藏状态h(t)决定。
* L(t)代表在序列索引号t时模型的损失函数。
* y(t)，代表在序列索引号t时训练样本序列的真实输出。
* U,W,V这三个矩阵模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。 也正因为是共享了，它体现了RNN的模型的“循环反馈”的思想。
** 隐藏层st=f(Uxt + Wst−1) ，st−1是前一时刻的隐藏状态， 通常函数f会选择tanh或者ReLU。
** 输出ot=Softmax(Vst)。
** 值得注意的是，虽然隐藏层状态的更新经历了全输入序列，但由于神经网络参数训练的机制，只有当前时刻前近段时间内输入对其有影响，这也是符合人类记忆的基本规律。

3. 前向传播算法

有了上面的模型，RNN的前向传播算法就很容易得到。

a） 首先是隐藏状态h(t)，对于任意一个序列索引号t， 由x(t)和h(t−1)得到：

其中σ为RNN的激活函数，一般为tanh,。另外b为线性关系的偏倚。

b） 其次序列索引号t时， 模型的输出o(t)的表达式比较简单：

c） 最终在序列索引号t时，预测输出为:

通常RNN是识别类的分类模型，所以上面这激活函数一般是softmax。

d） 通过损失函数L(t)，例如对数似然损失函数，就可以量化模型在当前位置的损失，即y^(t)和y(t)的差距。

5. 反向传播算法

有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。
RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数U,W,V,b,c。
由于是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。
这里的BPTT和DNN也有很大的不同点，即这里所有的U,W,V,b,在序列的各个位置是共享的，反向传播时更新的是相同的参数。

a） 为了简化描述，隐藏层的激活函数为tanh函数。输出的激活函数为softmax函数。损失函数为对数损失函数。

b） 对于RNN，由于在序列的每个位置都有损失函数，因此最终的损失L为：

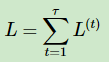
其中， V,c的梯度计算比较简单：

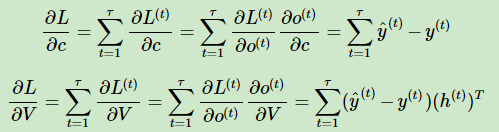
但是W,U,b的梯度计算就比较的复杂。
从RNN的模型可以看出，在反向传播时，在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置t+1时的梯度损失两部分共同决定。
对于WW在某一序列位置t的梯度损失需要反向传播一步步的计算。
定义序列索引t位置的隐藏状态的梯度为：

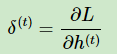
这样就可以像DNN一样从δ(t+1)递推δ(t) ：

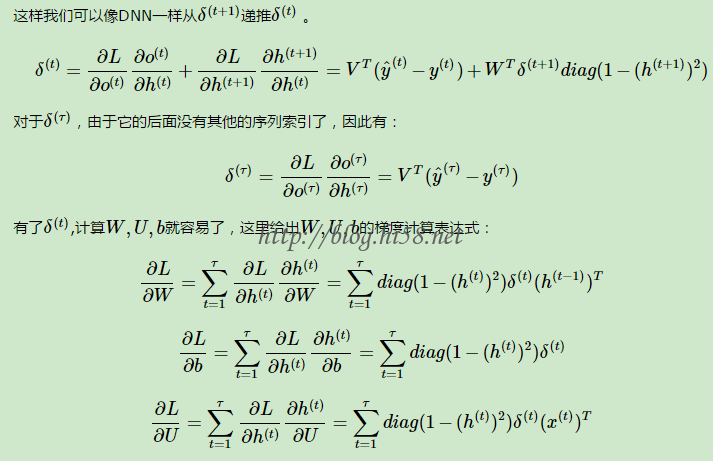
除了梯度表达式不同，RNN的反向传播算法和DNN区别不大。

7.
最简单的RNN就这样。
在此基础之上还有双向RNN和LSTM