44-卡尔曼滤波器基本原理

1、 马尔科夫链
2、 状态机
3、 概率加权
4、 示例
5、 工程模型
6、 工程模型实例
7、 Matlab实现实例

卡尔曼滤波，和傅立叶变换、泰勒级数一样，是用卡尔曼的名字命名的。
它的基础是Wiener的维纳滤波理论，但维纳滤波需要用到无限个过去的数据，并不适用于实时处理。
而卡尔曼把状态空间模型引入滤波理论，从而克服这一缺点。

1、 马尔科夫链

如果当前状态St仅仅与上一个状态St-1有关，而与上上个状态St-2无关，更与上上上个状态St-3没有关系…，那么这些状态就是马尔科夫链。
马尔科夫过程已经非常成熟的应用于语音识别、输入预测等等。比如在搜索框里输入清华，则可以自动填补出后面大学两个字，等等。

马尔科夫过程适合使用状态及描述。

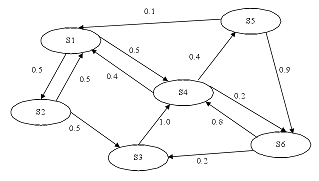
2、 状态机

卡尔曼的空间模型其实就是状态机。

例如，LabVIEW里面最重要的一个design pattern就是state machine状态机：
当前状态转换，依赖于上一状态。

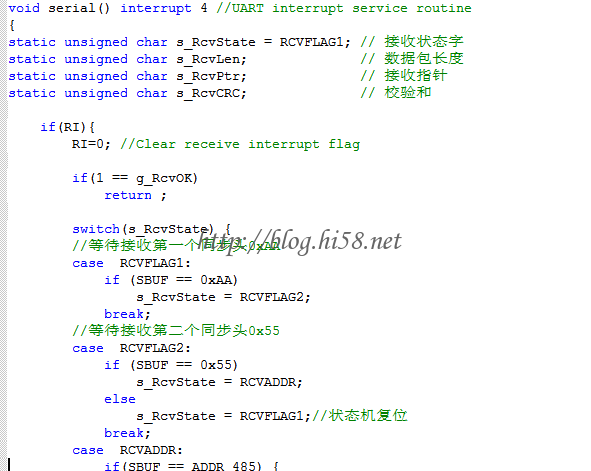
再例如单片机，其串口通讯协议一般都用状态机模型来组包：
当前接收的hex字符是不是有用数据，这要考虑上一个状态。当前字符需要根据上一状态，才能决定是有用数据、用于组建命令字，还是无用数据、可以直接丢弃：

3、 概率加权

卡尔曼滤波器是一个最优化的自回归算法，目标是最小均方误差，基本思想是采用信号与噪声的状态空间模型，利用前一时刻地估计值和现时刻的观测值来更新状态变量的估计值。
这有些智能算法的味道，比如遗传算法，不同之处在于卡尔曼没有用到随机数。

这个滤波算法在近几十年来已经应用到机器人导航、传感器数据融合等场景，最近年来也被应用于计算机图像处理，例如人脸识别、图像分割等。

总结：
卡尔曼主要是：一状态机、二概率加权、三迭代。

4、 示例

验证卡尔曼滤波，最好是用ds18b20温度传感器，搭上一块单片机开发板，尝试预测一下房间的温度试试，预测结果准确与否，立刻可以检验。
用来校正小车或者飞行器的姿态作示例，反而一时不容易看到直接效果。

假设研究对象为某房间的温度。
一、根据已有经验房间温度变化是缓慢的、甚至可认为恒定，也就是说，下一时刻温度等于现在时刻的温度。但是这个经验并不是百分百可靠，还可能有上下几度的偏差，这些偏差可以看作高斯白噪声，即偏差跟前后时间没有关系、而且高斯分布，此时就有了预测温度和预测偏差。

二、另外房间里放置有一支温度计（观测器），但是温度计也不十分准确，测量值与实际值也有偏差，偏差也呈高斯白噪声，此时就又有了观测温度和观测偏差。

三、那么在任意一时刻都存在两个温度值和两个偏差，一是根据经验的预测值和预测偏差，二是观测设备的观测值和观测偏差，而卡尔曼根据这两对值，就可以估算房间的最优温度和最优偏差，这又有了第三组数据。

四、注意，涉及的温度：预测温度、观测温度、最优（估算）温度。

下面以k时刻的估算为例。

已知：上一状态k-1时刻已经有估算出来的最优温度为23度最优偏差为3度，预测温度NA度预测偏差4度，当前状态k时刻的观测温度25度观测偏差4度，那么：

一、使用上一状态k-1时刻的数据。根据过去k-1时刻的最优温度23度，直接可得现在k时刻的预测温度等于23度，由k-1时刻最优温度23度的最优偏差是3度和k-1时刻预测温度NA的预测偏差是4度，间接可得当前状态k时刻的预测偏差为sqrt（3^2+4^2）=5度，这样当前状态k时刻的预测温度23度和预测偏差5度均已获得。

二、使用当前状态k时刻的数据。根据温度计得到当前k时刻的观测温度（例如25度），同时该观测温度的观测偏差是4度。这样当前状态k时刻的观测温度25度和观测偏差4度均已获得。

三、上两步已经获得当前状态k时刻的预测温度和观测温度两组数据，现在需要求取最关键的最优温度。对于由k-1时刻得来的预测值23度和根据k时刻温度计所得的观测值25度，应该相信预测多一点还是相信观测多一点，这需要用到协方差来判断，用的是卡尔曼增益Kg Kalman Gain，Kg大代表误差大的一方，它会反方向的增大误差小的那一方的可信度，即Kg的权重总是乘在较可信的那一方，你的误差越大给对方乘的权重越大。

首先构建卡尔曼增益Kg = sqrt[ 5^2/(5^2+4^2) ] = 0.78，通过 0.78*25 + (1-0.78)*23 = 24.56，就可以估算出当前状态k时刻的最优温度24.56度。

然后由sqrt[ (1-Kg) * 5^2 ]=2.35度，就可以估算出最优温度的最优误差是2.35度。这样，当前状态k时刻的最优温度24.56度和最优偏差2.35度均已获得。

四、可以看出，因为预测偏差比较大（5度）、观测设备温度计的covariance比较小（4度），所以还是比较相信温度计的观测数据，结果也表明估算的最优温度值是偏向温度计的观测值的。

五、重新列一遍，回忆一下由k-1时刻到k时刻的情况：

上一状态k-1时刻的最优温度为23度最优偏差为3度，预测温度NA度预测偏差4度，当前状态k时刻的观测温度25度观测偏差4度，

那么此时由k时刻到k+1时刻（黑体是发生变化了的数据）：当前状态k时刻的最优温度为24.56度和最优偏差2.35度，预测温度23度和预测偏差5度。

如果下一状态K+1时刻有了观测温度？观测误差4度，就可估算出k+1时刻的数据。如果有了K+1时刻就可估算出K+2时刻…手工演算两行：

其实就是迭代重新进入步骤一。

如果把分钟替换为天，把房间温度替换为城市温度，这其实就是一个简易的天气预报的模型。

5、 工程模型

工程系统上的卡尔曼滤波器算法，最核心的有5个计算公式。

首先，对于离散控制过程的系统，可用一个线性随机微分方程来描述：

X(k) = A*X(k-1) + B*U(k) + W(k)——关于系统的

Z(k) = H*X(k) + V(k)——关于观测的

X(t)是t时刻的系统状态，U(t)是t时刻对系统的控制量如果没有控制就是零，AB是过程参数，W(t)为过程噪声也就是预测偏差。Z(t)是t时刻的测量值，H是测量系统参数，V(t)为测量噪声也就是观测偏差。W(t)和V(t)两个噪声假设为高斯白噪声，它们的协方差分别是Q、R。

一、根据上一状态k-1时刻计算当前状态k时刻的预测值：

X(k|k-1) = A*X(k-1|k-1) + B*U(k) ——(1)

X(k-1|k-1)是上一状态k-1时刻已经估算出来的最优值，X(k|k-1)是利用k-1时刻预测k时刻的预测值，U(k)为当前状态k时刻的外加控制量、没有外部控制则为0，通过这个式子就更新了系统的状态。

二、还需要更新当前状态k时刻的预测值X(k|k-1)的协方差P：
P(k|k-1) = A*P(k-1|k-1) A’ + Q——(2)

P(k-1|k-1)是上一状态k-1时刻最优值X(k-1|k-1)的协方差，P(k|k-1)是当前状态k时刻预测值X(k|k-1)的协方差，Q是系统过程噪声的协方差即预测偏差。

三、然后由当前状态的观测值，结合预测值，得到当前状态k时刻的最优值X(k|k)：

X(k|k) = X(k|k-1) + Kg(k)*(Z(k) – H*X(k|k-1)) ——(3)或者表达为：

X(k|k) = [I – Kg(k)*H] * X(k|k-1) + Kg(k)*Z(k) ——(3)

Z(k)是当前状态的观测值，Kg位卡尔曼增益，此时已经估算出了当前状态的最优值X(k|k) 。这个式子比较关键。

四、更新卡尔曼增益Kg：

Kg(k) = P(k|k-1) *H’ / (H*P(k|k-1) H’ + R)——(4)

P(k|k-1)是当前状态k时刻预测值的协方差，R是观测过程噪声即观测偏差。

五、虽然已经得到了k状态下最优数据X(k|k)，但是为了迭代需要还要更新当前状态k时刻最优值X(k|k)的协方差：

P(k|k) =（I-Kg(k)*H） * P(k|k-1)——(5)

I为单位矩阵，或者对单变量就是标量1。

注意含义：P(k|k)是当前状态k时刻最优值的协方差，而P(k|k-1)是当前状态k时刻预测值得协方差。

六、不停递归即可：k、k+1、k+2…

6、 工程模型实例

前面上好佳实例里面，房间就是系统，对于该系统：只有一个变量，即温度；当前状态温度等于上一状态温度，所以系统参数A=1；没有外部控制，所以U(k)=0，系统参数B自然不需考虑。因此该系统的过程是：

X(k|k-1) = X(k-1|k-1)——式子1

上好佳实例里面，观测器就是温度计。因为温度计测量值就是温度不需变换，所以该系统的观测窗口H=1：

P(k|k-1) = P(k-1|k-1) + Q——式子2，Q过程噪声协方差

其他三个式子依次是：

X(k|k) = X(k|k-1) + Kg(k)*(Z(k) – X(k|k-1)) ——式子3或者表达为：

X(k|k) = [1 – Kg(k)] * X(k|k-1) + Kg(k)*Z(k) ——式子3

Kg(k) = P(k|k-1) / (P(k|k-1)  + R)——式子4，R观测噪声协方差

P(k|k) =（I-Kg(k)） * P(k|k-1)——式子5

7、 Matlab实现实例

m代码：

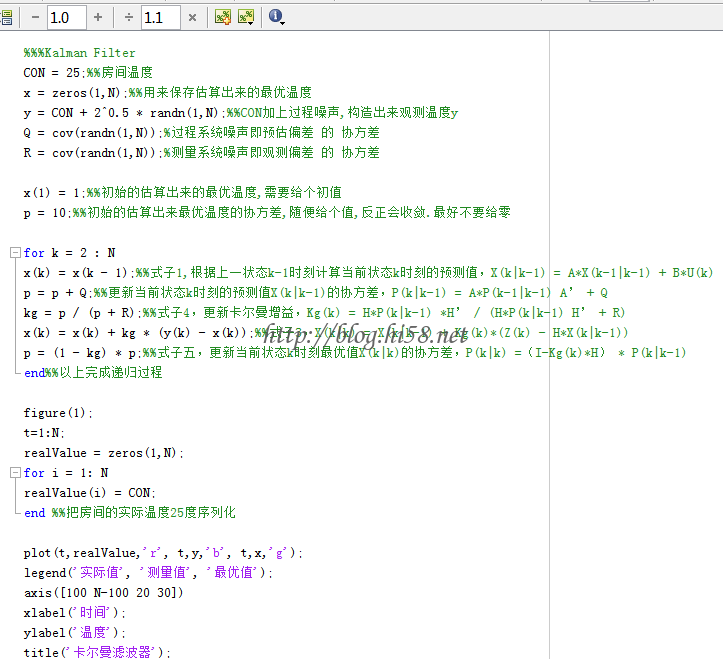
效果：

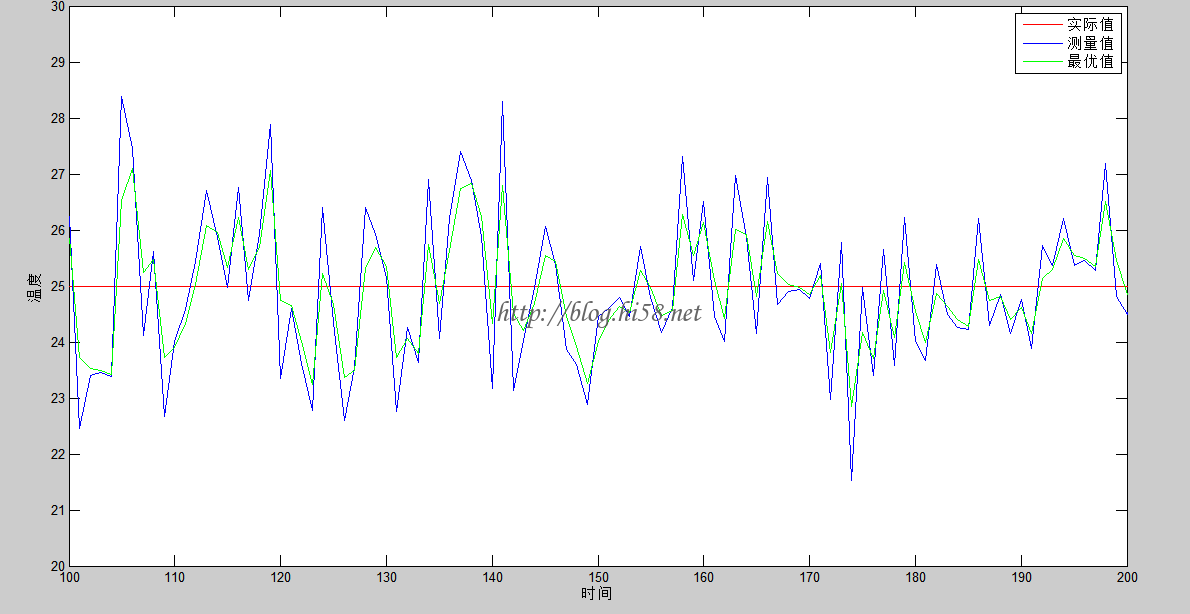
对于这种简单温度预测的算法，用C实现比较简单。

补充：
以上的协方差是广义的，很多时候就是方差，不是协。一个变量的方差可以理解成该变量和变量本身的协方差，并没错误。