机器人姿态（07）：姿态获取（续）

从类似小米平衡车里面的MPU，可以计算得到几个不同的小车倾角，分别是根据加速度计算出的倾角、根据陀螺仪计算出的倾角和互补算法计算出的倾角、卡尔曼算法计算出的倾角。

• 加速度计算的角度

加速度计可以测量某时刻XYZ三个方向的加速度值，而通过重力加速度在XYZ三个轴的分量，就可以计算出小车的倾角。

不过小车在非静止状态下，加速度计测得的结果并不非常精确。因为小车在动态时受电机作用还有前进或者后退的力，所以加速度计测得是总的加速度。这表明加速度数据在静态下才准确，不过好消息是陀螺仪在动态下的数据准确，所以需要综合加速度计的加速度数据和陀螺仪的角速度数据才会更准确，这些是所谓的互补算法或卡尔曼滤波算法。

从简单的开始，把MPU平放在车体上，定义X为前进方向，则Y轴平行于左右车轮的轴线，如下图：

可见车体Y轴与地平面夹角是不会发生变化的，一直为0度。能发生变化的是X轴与平面的夹角，或者说Z轴与平面的夹角，可以证明X轴Z轴夹角变化是一致的。下面抛开上面的透视图，采用正试图来看：

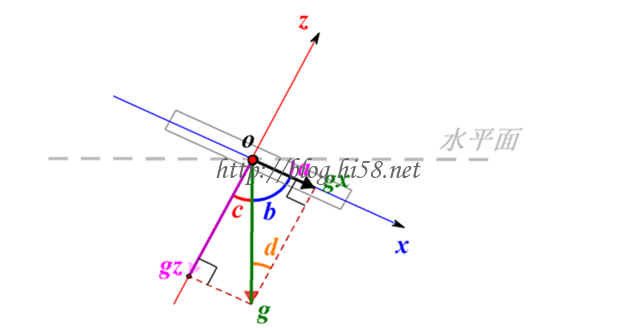
上图中，g为重力加速度，gx和gz为MPU测得的加速度数据，但同时也是重力加速度在x和z轴的分量。

很容易看出小车倾角就是atan（gx/gz），实际使用考虑到零点偏移：Angle_Z = (AccZ – AccZ_Offset) * R_Z。

其中AccZ是Z轴加速度实时测得的数据，AccZ_Offset是Z轴加速度的静差，R_Z是加速度计Z轴比例系数。

上面是用的三角函数的反正切函数，从数值计算角度也可以用asin（gx/g），因为在小角度时候有sin（dalpha）=alpha的近似（弧度方式）成立。角度方式是sin（alpha）=alpha*pi/180，MPU给出的是后面这种角度方式。经过拟合试验后可以进一步作修正：sin（alpha）=0.92*alpha*pi/180，因此由gx/g=sin(alpha)=0.92*alpha*pi/180，可以得角度alpha=180*gx/0.92*pi*g，这是个近似的方法，这个数据不很准确，单是速度快。

• 陀螺仪计算的角度

通过陀螺仪计算角度很简单，陀螺仪测得的是角速度，角速度乘某段时间就是该段时间所转过的角度，如果再把每次计算所得的角度累加（积分）就得到当前位置的倾角了。

假设，陀螺仪是最初平行于桌面，单片机每delta_t时间读一次陀螺仪的角速度，读三次以后 Z轴顺时针转到下图中位置：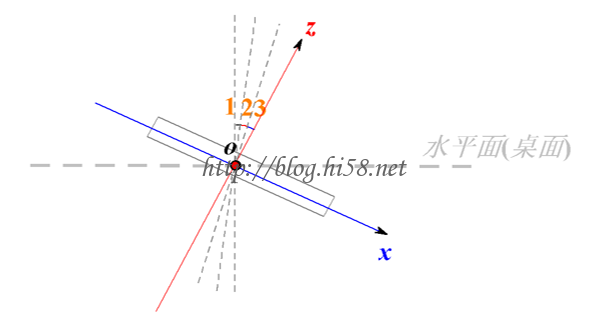

那么这段时间内转过的总角度为角1+角2+角3，如果陀螺仪测得的角速度分别为w1/w2/w3，则总角度为w1*delt_t1+w2*delta_t2+w3*delta_t3，这其实就是个离散积分的过程，一般写成：angle_n =  angle_n-1 + (Gyro – Gyro_Offset) * R_Gyro。

其中angle_n是当前角度值，angle_n-1是上次计算所得的角度。Gyro是陀螺仪实时测得角速度，Gyro_Offset是陀螺仪零点偏移值。R_Gyro是陀螺仪比例。

但陀螺仪计算所得的角度也存在误差，而且误差越积累越大，最终导致计算角度与实际角度相差很大，因此需要考虑加速度计算的角度。

•  互补算法计算的角度

 //一阶互补算法
factor = 0.095;
K =factor / (factor + delta_t);   //K开始时0.98
angle_Comp1 = K * (angle_Comp1 + omega * delta_t) + (1-K) * angle_Acc;
// 二阶互补算法
factor = 0.2;
x1 = (angle_Acc – angle_Comp2)*(1-factor)*(1-factor);
y1 = y1 + x1 * delta_t;
x2 = y1 + 2 * (1-factor) *(angle_Acc – angle_Comp2) + omega;
angle_Comp2 = angle_Comp2 + x2 * delta_t;

• 卡尔曼算法计算的角度

angle_Kalman += (omega – Gbias) * delta_t;  //先验估计

Pdot[0] = -PP[0][1] – PP[1][0] + Q_angle;
Pdot[1] = – PP[1][1];
Pdot[2] = – PP[1][1];
Pdot[3] = Q_gbias;//

PP[0][0] += Pdot[0] * delta_t;
PP[0][1] += Pdot[1] * delta_t;
PP[1][0] += Pdot[2] * delta_t;
PP[1][1] += Pdot[3] * delta_t;     //先验估计误差协方差

PCt_0 = C_0 * PP[0][0];  PCt_1 = C_0 * PP[1][0];
E = R_angle + C_0 * PCt_0;

if(E!=0) {
K_0 = PCt_0 / E; K_1 = PCt_1 / E;
}

PP[0][0] -= K_0 * PCt_0;
PP[0][1] -= K_0 * PCt_1;
PP[1][0] -= K_1 * PCt_0;
PP[1][1] -= K_1 * PCt_1;      //后验估计协方差

angle_Err = angle_Acc – angle_Kalman;
angle_Kalman += K_0 * angle_Err;    //后验估计
Gbias += K_1 * angle_Err;