1、 贝叶斯统计
2、 贝叶斯分析
3、 贝叶斯决策
4、 朴素贝叶斯的分类算法
5、 最大似然估计和贝叶斯估计
6、 示例 – 似然函数
7、 示例 – 后验概率

1、 贝叶斯统计

案例：
驾驶员车窗结露看不清前方、仅依靠后视镜、发现后车亮起了右转向灯，问：此时本车处在右转车到（即需要右转）的概率是多少？

用A表示本车位于右转道路口，B表示后车右转向灯亮，则：
先验概率P(A) ：
即没有依靠其他信息、此时在此路段碰到了右转车道的概率。这根据这个路段位于北京还是西藏区别很大。
条件概率P(B|A)：
即处于右转路口，而且又主动打右转向灯的概率。 因为当然有司机在右转道要转弯、但是却不打转向灯，还有的不在右转车道，却也打着右转向灯不停，这些情况都有。
后验概率P(A|B)：
即需要求解的看到了右转向灯亮、而且位于右转车道，这个后验概率。

上面的先验概率P(A)、条件概率条件概率P(B|A)、最终得到后验概率P(A|B)，是贝叶斯统计的三要素。

根据P(A)、P(B|A)，就可以由贝叶斯定理：
P(A|B) = P(B|A)P(A) / P(B)
计算出看到右转灯亮、且处于右转车道路口这个后验概率P(A|B)。

2、 贝叶斯分析

贝叶斯分析是根据证据的积累来推测一个事物发生的概率，当预测一个事物时，需要先根据已有的经验和知识推断一个先验概率， 然后在新证据不断积累的情况下调整这个概率，这个通过积累证据从而得到一个事件发生概率的过程，称为贝叶斯分析。

理解贝叶斯分析最好的方法是图像法， 这图里，红圈A占大圈的比例，即先验概率P(A)， 小阴影AB占蓝圈B的比例，即后验概率P(A|B)。

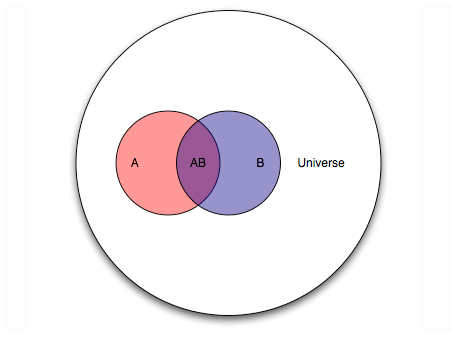
先验概率，即取得证据之前的概率P（A），这个通常来自之前的经验常识，带有一定的主观色彩。
注意: 先验概率在贝叶斯统计中具有重要意义，不可忽视。

例如：
发现一些没读过书的人很有钱，事实是当发现时就已经是幸存者了（对应上图中的红圈）， 而死了的人（红圈外的大部分面积）都忽略了啊。
再例如：
由一个人着装雅致，推断他是大学教授还是工程师，这里也得仔细注意先验了，即：在整个人群中大学教授多、还是工程师多，也就是红圈和大圈的关系。

这个图，红圈和篮圈的比例， 很少能在开始就知道， 这是应用的难点：
回前面案例，
如果恪守先验概率，就会无视变化、墨守成规、直接忽视右转向灯亮的信号；
如果过于注重特例，完全不看先验概率，很可能把噪声当成信号，看到灯就转向。

A即位于右转车道，
B是看到后车右转向灯亮，
A|B即右转向灯亮且位于右转车道，
B|A是位于右转路口且打起右转向灯。

这个案例里：
根据路段位于北京繁华区域、结合经验、设定：
P（A）=5%，即：这条路段5%可能是右转车道，其余95%部分是直行车道、或者处在左转车道。
P（B|A）=20%，即：位于右转车道的人20%会打起右转向灯，其余的呢可能是从右转道直行走了、或从右转道左转了、或者从右转道确实右转了但是没打右转向灯。

那么如果假设P(B) = 2%， 即在整个车辆行驶过程中，有2% 的概率右转弯灯亮了。

那么复制一下贝叶斯定理：
P(A|B) = P(B|A)P(A) / P(B)
换一下;
P(A|B) = P(A) * P(B|A)/ P(B)
= 5% * 20%/2% = 50%

可见：
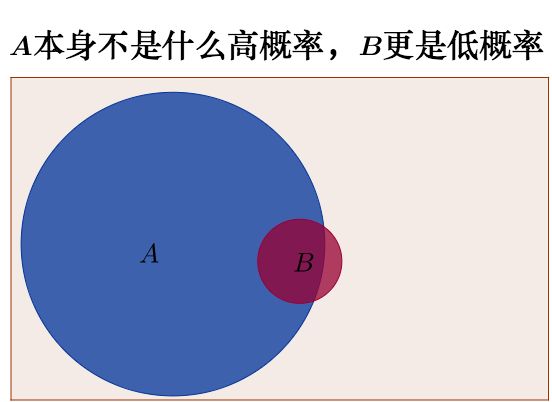
原来的先验概率P（A）=5%，即此时恰好位于右转车道的概率为5%，并不高；
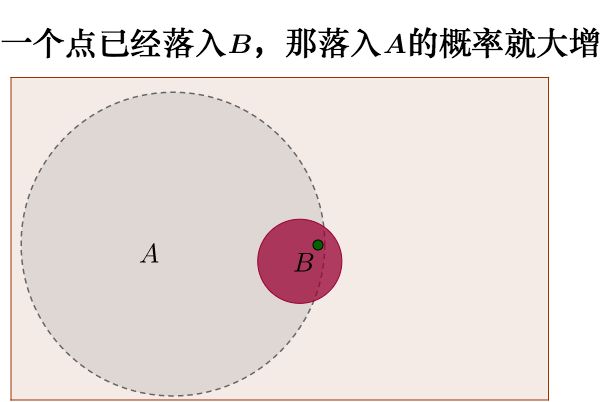
而由于公式右侧一项的贡献、即看到右转向灯亮， 则后验概率P(A|B)提升到了50%。

即：
新信息出现之后的A的概率 = 原来A的概率 * 新信息带来的调整。

新信息出现前：

新信息出现后：

3、 贝叶斯决策

基于贝叶斯分析，可以引出贝叶斯决策，它主要包含四部分：
数据D、假设W、目标O、决策S。

此处：
数据，即之前讲到的证据，
假设，是要验证的事实，
目标，是最终要取得优化的量，
决策，是根据目标得到的最后行为。

一般步骤是：
理清因果：哪个是假设、哪个是证据，
给出所有可能假设、即假设空间，
给出先验概率，
根据贝叶斯公式求解后验概率，得到假设空间的后验概率分布，
利用后验概率求解条件期望，得到条件期望最大值对应的行为。

以上转化成算法就是机器学习。

4、 朴素贝叶斯的分类算法

案例：
给出某人的身高和体重，判断其性别？

首先：证据是身高和体重，假设是性别男类型，
其次：先验概率是人口中的男女比例，条件概率是男性和女性的身高和体重分布。
然后，可以根据贝叶斯公式求解后验概率。
最后，要做的决策是性别分类，目标是分类错误率最低。

贝叶斯决策是构建有监督机器学习的重要基础。
例如前述性别问题：
在训练部分，根据已有数据求出不同性别对应身高和体重的概率分布；
在测试部分，用朴素贝叶斯分类器进行决策。

5、 最大似然估计和贝叶斯估计

事实上， 贝叶斯决策很少只涉及A和B，而是内部包含非常关键的隐变量（参数），涉及对所研究事物的一些基本预设。

例如最简单的：抛硬币10次、出现9次正面1次背面，对这个问题：
频率学派，认定出正面的概率为0.5不变，否定0.5的想法是匪夷所思；
贝叶斯学派，需要把这个（隐）变量看成是未知的参数（具有一定先验概率），之后按照贝叶斯公式调整新加入证据对先验概率的影响。

要注意：
此处先验概率十分重要，它影响决策的结果，因为：
如果先验的认为出正面概率为0.5，那么需要得到大量偏离0.5的证据之后，才能逐步纠偏。

总结：
最大似然估计把参数看做是确定（非随机）而未知的，最好的估计值是在获得实际观察样本的概率为最大的条件下得到的。
贝叶斯估计是把参数当做具有某种分布的随机变量，样本的观察结果使先验分布转换为后验分布，再根据后验分布修正原先对参数的估计。
这两者在结果上通常是近似的，但概念上它们的处理方法完全不同。

6、 示例 – 似然函数

游戏规则：
押一块钱，可以抛10次硬币，出现正面的次数小于等于6次、就赢得一块钱，大于6次正面则输掉的一块钱。

定义随机变量：
Y ：表示出现正面的次数
X ：表示一局输赢结果
X = ：
1 if Y<=6 0 if Y>6

赢了之后，一块钱就变成了两块钱；输了之后，一块钱就变成了没有钱；
定义函数f(X)表示游戏之后的结果：
f（X）= ：
2 if X=1
0 if X=0

增加常识：
* 抛硬币出正面的概率，等于出现反面的概率，等于0.5。
* 第一次抛硬币的结果 不会影响 第二次抛硬币的结果，验的结果是相互独立的。
* 这是一个可重复的试验，结合上面这点就是一个独立可重复试验。

二项分布常用来对独立可重复实验进行概率建模，所以这个抛硬币服从二项分布B(N,p)。
N是进行的实验的次数10，p可以用r代替表示抛一次硬币出正面的概率在这里是r=0.5，用Y表示出现正面的次数，则：
P（Y=y） = C（N，y）* r^y * (1-r)^(N-y)

根据假设：
N=10，r=0.5，得P(y<=6) = P(y=0)+…P(y=6) =0.8281，意味着有0.8218的概率赢。 赢到的数额期望是： E{f(x)} = 2*0.8281 + 0*(1-0.8281) = 1.6562 也就是说在抛硬币出现正面和反面概率相同都为0.5的情况下，根据游戏规则最终能得到1.6562块钱。 上面，最重要的先验信息是： 抛一次硬币，出现正面和反面的概率是一样的都为0.5。 现在，换种思路： 万一硬币被做了手脚，抛出正面的概率不是0.5呢？ 如果按照贝页斯分析，需要把r也视为一个随机变量，那么N次独立重复的抛硬币实验的概率分布函数，可写成条件概率的形式： P( Y=y|r,N) = C(N,y) * r^y * (1-r)^(N-y) 此时，在 r 未知的情况下，拿到了一组实验数据(样本信息)，有个人他抛了10次硬币，出现了9次正面1次反面。 那么还有多少理由相信r=0.5？ 由二项分布概率密度: P( Y=y|r,N) = C(N,y) * r^y * (1-r)^(N-y) 那么r为多少才能让P(Y=y|r,N)在y=9时取最大值？ 去对数不影响指数函数的单调性： L = ln P(Y=y|r,N) = ln C(N,y) + y*ln(r) + (N-y)*ln(1-r) —>MAX
L可称为对数似然函数。

对r求偏导数即获得极值点：
dL/dr = y/r – (N-y)/(1-r)
这里用d表示偏导。

当y为9时，r=0.9。

此时：
得P(y<=6) = P(y=0)+…P(y=6) =0.0128，意味着游戏有0.0128的概率赢。

此时的期望：
E{f(x)} = 2*0.0128+ 0*(1-0.0128) = 0.0256
也就是说在抛硬币出现正面概率为0.9的情况下，根据游戏规则最终能得到0.0256块钱。

以上过程是：
首先，先验分布设定为0.5，
然后，确定模型为二项分布，
以及，模型参数为r，
最后，似然求解得参数为0.9。

7、 示例 – 后验概率

REF：
http://www.woshipm.com/pmd/421033.html
http://www.cnblogs.com/hapjin/p/6653920.html
https://www.zhihu.com/question/19725590/answer/217025594