37 – 贝叶斯滤波

1、 全概率公式
2、 贝叶斯公式
3、 贝叶斯公式解释
4、 公式的简化
5、 多观测数据融合
6、 动作的影响
7、贝叶斯滤波
————-

1、 全概率公式

p(x) = ∑ p(x|y)p(y) OR p(x) = ∫p(x|y)p(y)dy

全概率公式的意义是：
如果直接计算p(x)困难，而存在yi恰好可以两两互斥的划分样本空间， 并且p(yi)的计算更简单，就可以利用全概率公式计算p(x)。

全概率公式的思想是：
将事件x分解成几个小事件，求这各个小事件的概率，对其相加，从而求得事件x的概率。

所以，在将事件x进行分割时，不是直接对X进行分割，而是先找到样本空间的一个划分y1,y2…yn，这样事件X就被分解成了事件xy1,xy2…xyn这样n部分，即x = xy1+xy2+…+xyn, 每一个yi的发生可能导致x发生的概率是P(x|yi)。

例如：
甲、乙、丙三台机床次品率为5%，4%，2%，这三台的产出量占总体的25%，35%，40%，在总体产品任取一个产品为次品的概率？
p(x) = 25%*5%+4%*35%+2%*40%=0.0345

2、 贝叶斯公式

由条件概率公式： p(x|y) = p(x,y) / p(y)
并结合乘法公式： p(x,y) = p(x|y)p(y) = p(y|x)p(x)
可得贝叶斯公式： p(x|y) = p(y|x)p(x) / p(y)

贝叶斯公式与全概率公式解决的问题是相反的：
它是建立在条件概率的基础上寻找事件发生的原因，即大事件y已经发生的条件下，分割中的小块事件xi的概率。

假设xi是样本空间的一个划分，这些xi通常是结果y出现的原因之一；
p(xi)表示各种原因出现的可能性大小，称先验概率；
p(xi|y)反映了在结果y出现之后，再对各种原因xi概率的新认识，称后验概率。

例如：
发报机以概率0.6和0.4发出信号+和-。由于干扰，发+时收报台以概率0.8和0.2收到信号+和-，发-时收报台以概率0.9和0.1收到信号-和+。现收报台收到+，问发报机确实发出+的概率？
p(x=+|y）= (0.6*0.8)/(0.6*0.8+0.4*0.1) = 0.923

3、 贝叶斯公式解释

贝叶斯公式：
p(x|y) = p(y|x)p(x) / p(y)

这里：
x一般是某种状态。
y一般是某种观测。
p(x)这个先验概率，是对x的先验知识，例如一扇门开着的概率为50%。
p(y|x)这个条件概率，意思是由状态x已知可以推算观测数据y的概率这种因果关系。例如已知门开状态，则测距仪读数z=0.6m；若门关的话，测距仪数据z=0.3。
p(x|y)这个后验概率，是基于观测数据获取后而对状态的推断，它是由先验概率和从因到果的条件概率而计算出来的。

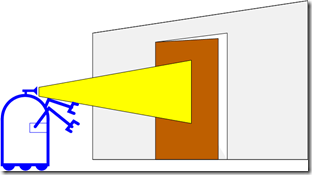
例如图中示例：
机器人的测距仪读数z=0.5m，问门的状态开open或非开~open的概率？
p(door=open|z=0.5) <---这里的后验概率p(open/z)由下一行的贝叶斯公式计算 = ∑[p(z|open)p(open)] / p(z) <--- 这里的观测数据概率p(z)由下一行的全概率公式计算 = 0.6*0.5 / ∑[ p(z|door)p(door)] = 0.3 / ( p(z|door)p(door=open) + p(z|door)p(door=~open) ) = 0.3 / (0.6*0.5 + 0.3*0.5) = 2/3 这里p(z)的全概率计算，=p(z|door)p(door=open) + p(z|door)p(door=~open) = 0.6*0.5 + 0.3*0.5， 可见仅基于先验概率和条件概率，是常数项了， 所以有简化计算方法。 4、 公式的简化 贝叶斯公式： p(x|y) = p(y|x)p(x) / p(y) 式中分母p(y)常项可以归一化系数处理， 成为： p(x|y) = p(y|x)p(x) / p(y) = K p(y|x) p(x) （由全概率得此处K = 1/p(y) = 1/∑ p(y|x)p(x) ） 5、 多观测数据融合 单一传感器或单次数据y未必可靠， 有时要融合多个传感器数据或单传感器的多个读数y1，y2...来确定x的状态。 继续上面示例： 机器人又读了第二次，测距仪读数z=0.5m，问门的状态开open或非开~open的概率？ 要注意此时门状态概率已经不是开50%关50%，而是由于有了第一次的观测读数，已经变为开2/3关1/3这样的概率分布了。 （前面求出来的后验概率2/3，这里就成先验概率了。） p(door=open|z=0.5) <---这里的后验概率p(open/z)由下一行的贝叶斯公式计算 = ∑[p(z|open)p(open)] / p(z) <--- 这里的观测数据概率p(z)由下一行的全概率公式计算 = 0.6*2/3 / ∑[ p(z|door)p(door)] = 0.4 / ( p(z|door)p(door=open) + p(z|door)p(door=~open) ) = 0.4 / (0.6*2/3 + 0.3*1/3) = 4/5 可见增加的第二个观测数据把门处于开状态的概率由2/3提高到4/5。 以下公式推导， 对于贝叶斯公式： p(x|y1) = p(y1|x)p(x) / p(y1) 如果增加第二个新的观测数据y2： p(x|y2,y1) <---根据条件概率公式 = p(x,y2,y1)/p(y2,y1) <---对分子第一项根据乘法公式 = p(y2|x,y1)p(x,y1)/p(y2,y1) <--- 对分子第二项根据乘法公式 = p(y2|x,y1)p(x|y1)p(y1)/p(y2,y1) <--- 对分母根据乘法公式 = p(y2|x,y1)p(x|y1)p(y1)/p(y2|y1)p(y1) <---消项 = p(y2|x,y1) p(x|y1) / p(y2|y1) 再增多观测数据的话，可把上式的y1扩展为观测数据y1，y2，...yn-1，y2为最后增加的这个观测数据yn： p(x|yn,…,y1) <--- 带入上式 = p(yn|x,yn-1,…,y1) p(x|yn-1,…y1 ) / p(yn|yn-1,…y1 ) <---yn和yn-1,...y1无关 = p(yn|x) p(x|yn-1,…y1 ) / p(yn|yn-1,…y1 ) <---移动个位置 = p(yn|x) / p(yn|yn-1,…y1 ) * p(x|yn-1,…y1 ) <---第一项的分母常数项 = Kn p(yn|x) * p(x|yn-1,…y1 ) <---最后一项就可以同型迭代了 = Kn p(yn|x) * Kn-1 p(yn-1|x) *... * p(x|y2,y1) = Kn p(yn|x) * Kn-1 p(yn-1|x) *... * K2 p(y2|x) * K1 p(x|y1) = Kn*Kn-1...K1 * p(yn|x)*p(yn-1|x)...p(y1|x) * p(x) 这里p（x）是已知的先验概率，例如门开概率4/5； p(y1|x)为已知的条件概率，例如门若开激光测距仪应读数为0.6m（y1）、门若开红外测距仪读数应为0.9m（yn）、...等。 6、 动作的影响 以上对于系统已经讨论了自身状态x， 传感器观测y，但缺少控制动作t。 在Bayes模型中的动作t的影响，也就是在x′状态下执行动作t后状态改变到x的概率： p(x|t,x′)。 动作对状态的影响， 一般用状态转移模型描述。
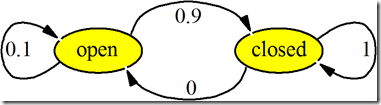
上图转移模型表示了关门动作对状态的影响。既：如果门处于开状态，关门动作后门有0.9的概率成功处于关状态、有0.1的概率失误仍保持为开状态；若门是关状态，执行关门动作后有1.0概率出于关闭状态、有0概率出于开状态。

那么执行动作后的状态xn的概率计算，要考虑动作t之前的所有状态xn-1，即使用权概率公式：
p(x|t)= ∑ p(t|t,xn-1)p(xt-1)

继续前例：
在经过两次传感器观测后已经计算获得门开概率为4/5，此时执行一次关门操作，动作之后门开的概率多少？

p(door=open|t,x)
= ∑ p(open|t,xn-1)p(xt-1)
= p(open|t,open)p(d=open) + p(open|t,close)p(d=close)
= 0.1*4/5 + 0*1/5
=0.08
执行一次关门动作后，门状态为开的概率是0.08。

7、贝叶斯滤波

对一个系统：
有了系统状态：p(x)，这个先验概率分布。例如门开门关的概率分布
有了观测模型：p(y|x)，这个条件概率。例如门若开测距仪数据0.6m若关闭数据0.3m
有了状态模型：p(x|t,x′)，这个可用全概率计算的状态转换图。
还有了1…n时刻的观测和动作数据：：Dn–> {t1,y1,…tn,yn}

那么，就可以计算输出的后验的状态概率：
BEL(xn) = p(xn |t1,y1,…tn,yn)
这个BEL是believe，置信的意思。

这个滤波器需要一些假设：
n时刻的观测yn，仅决定于n时刻的状态xt，与xt-1、xt-2无关。
n时刻的状态xn，决定于n−1时刻的状态xn-1和n时刻的动作tn，与xn-2、xn-3…无关。
以上即马尔科夫性，还要假设：
模型的噪声相互独立。
观测的噪声相互独立。

贝叶斯滤波的迭代形式：
BEL(xn)
= p(xn |t1,y1,…tn,yn) <--根据多观测的贝叶斯公式，置换yn = K*p(yn|xn,t1,y1,...tn) p(xn|t1,y1,...tn) <--根据马尔科夫性，yn与t1,y1,...tn无关 = K*p(yn|xn) p(xn|t1,y1,...tn) <--根据状态转移概率对xn求全概率，xn-1互斥划分样本空间 = K*p(yn|xn) ∑[ p(xn|t1,y1,...tn-1,yn,tn, xn-1) p(xn-1|t1,t1,...tn-1,yn-1,tn) ] <--根据马尔科夫性，xn仅与xn-1和tn有关 = K*p(yn|xn) ∑[ p(xn|tn, xn-1) p(xn-1|t1,t1,...tn-1,yn-1,tn) ] <--根据马尔科夫性，xn-1和tn也无关 = K*p(yn|xn) ∑[ p(xn|tn, xn-1) p(xn-1|t1,y1,...tn-1,yn-1) ] <--后面这就出现迭代形式 = K*p(yn|xn) ∑[ p(xn|tn, xn-1) BEL(xn-1) ] 可见，贝叶斯滤波器，最终表现成两部分： 对于观测数据，则更新状态，p(yn|xn) ，基于新的观测数据更新了yn|xn这个条件概率分布。 对于动作数据，则预测状态，∑[ p(xn|tn, xn-1) BEL(xn-1) ]，基于转移模型xn−1、tn预测了xn的条件概率分布。 伪代码： FILTER( BEL(x), D ): K=0 IF D is sensor data then: FOR all x do: BEL_NEW(x) = p(y|x)BEL(x) K = K+BEL_NEW(x) FOR all x do: BEL_NEW(x) = BEL_NEW(x) / k ELSEIF D is action command then: FOR all x do: BEL_NEW(x) = ∑[ p(x|t,x') BEL(x') ] ENDIF return BEL_NEW(x) 从代码可见： 如果要进行状态预测，需要遍历所有可能的x′状态，计算量很大。 而且如果BEL（x）是任意分布，更需要在xn所有可能取值点上计算该取值的概率，实现很难。 所以， 在应用时一般要对BEL（x）的分布进行假设来近似，从而衍生一些实用算法： 卡尔曼滤波 KF， 信息滤波 IF， 粒子滤波 PF。 REF： http://in.ruc.edu.cn/pc2016/