42 – 贝叶斯滤波到卡尔曼滤波

1、 正态分布
3、 模型假设
4、 模型方程
5、 模型参数
6、 算法伪代码
7、 贝叶斯推导
8、 结束
————-

把前面的离散贝叶斯滤波器：
BEL(xn) = K*p(yn|xn) * ∑[ p(xn|tn, xn-1) BEL(xn-1) ]
应用在连续系统就是：
BEL(xt) = K*p(yt|xt) * ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1)
即：
求和为积分、离散n为连续t，动作t用u代替避免时间序列符号t。

为了实用和计算效率， 需要对BEL（x）进行分布假设。

例如：
假设BEL（x）服从正态分布，则不再需要逐点采样并计算xt，只要随时掌握均值和方差两个参数，就可以获得BEL（x）的全部信息了，这样把对xt逐点的迭代计算变为两个参数的迭代计算。这样就成为了“卡尔曼滤波器”。

1、 正态分布

一元正态分布：
p(x) ∼ N(μ,σ 2 )， 即：
p(x) = 1/[sqrt(2π)*σ] * exp[ −1/2*(x−μ)^2/σ^2 ]

正态分布的特点：
分布的形态完全由一阶矩即均值和二阶矩即方差完全决定。
正态分布的线性组合仍为正态分布。

3、 模型假设

卡尔曼滤波解决的是动态系统的状态追踪问题，基本假设是：
状态方程是线性的。
观测方程是线性的。
过程噪声符合零均值高斯分布。
观测噪声符合零均值高斯分布。
这样保证了一直在线性空间中操作高斯分布，状态的概率密度符合高斯分布。

4、 模型方程

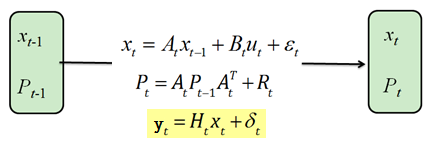
xt = At*xt−1 + Bt*ut + εt
Pt = AtPt-1At` + Rt
yt = Ht*xt + δt

5、 模型参数

xt： n*1的向量，对应在t时刻1…n个状态量的均值，例如门1开、门2开…
yt： m*1的向量，表示在t时刻的1…m的传感器的观测值，例如测距仪1、测距仪2…
ut： l*1的向量，表示在t时刻的l…l个输入动作
εt： n*1向量，过程噪声，符合零均值高斯分布
δt： m*1观测噪声，符合零均值高斯分布
Rt： n*n矩阵，表示过程噪声εt的方差矩阵
Qt： m*m矩阵，表示观测噪声δt的方差矩阵
At： n*n矩阵，表示n个状态量从t−1到t在没有输入影响时的转移方式
Bt： n*l矩阵，表示在t时刻ut对状态xt的影响
Ht： m*n矩阵，表示状态xt如何被转换为观测yt
Pt： n*n的差矩阵，表示t时刻被观测的1…n个状态量的方差。
Kt： n*m增益矩阵，这增益矩阵式卡尔曼纳的核心

6、 算法伪代码

KALMAN_FILTER( xt-1,Pt-1, ut,yt):
prediction：
xt_bar = At*xt-1 + Bt*ut <---预测t时刻状态，基于状态转移矩阵At和输入控制ut Pt_bar = At*Pt*A`t + Rt <---预测方差矩阵， correction： Kt = Pt_bar*H`t* (Ht*Pt_bar*H`t +Qt)^-1 <---更新增益矩阵，观测噪声方差Qt越大增益Kt越小 xt = xt_bar + Kt(yt - Ht*xt_bar) <---更新状态，基于新的观测信息 Pt = (I - Kt*Ht)*Pt_bar <---更新状态的方差矩阵。 END 其中：下标_bar为计算均值，上标`为转置，^-1为逆。 倒数第二个式子：xt = xt_bar + Kt(yt - Ht*xt_bar) (yt − Ht*xt_bar)表示观测值yt与预测值Ht*xt_bar的差； 再乘子Kt，表示观测yt的噪声大的的话，就采信的比较小。然后拿这个小的修正xt_bar。 即增益和噪声相反趋势。 相反，如果观测yt的噪声比较小，预测Ht*xt_bar的误差比较大，则乘以Kt后的修正幅度比较大，因为观测的噪声小、可靠。 再如果，观测yt的噪声小、预测的Ht*xt_bar的误差也小，那么修正幅度也不大。 总结： 就是利用观测数据修正预测数据。 准确的观测的修正量大，不准确的观测的修正量小。 所以误差较大的时候能快速修正，在误差较小时能逐渐收敛。 7、 贝叶斯推导 7.0 基础是基于： 离散贝叶斯滤波： BEL(xn) = K*p(yn|xn) ∑[ p(xn|tn, xn-1) BEL(xn-1) ] 应用在连续系统： BEL(xt) = K*p(yt|xt) * ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1) 7.1 系统初始状态是： BEL(x0) = N(miu0, P0 ) 7.2 预测过程 状态转移模型是： xt = At*xt−1 + Bt*ut + εt 由于这是个线形函数，所以从xt−1 到 xt的状态转移概率（条件概率）也高斯分布: *** p(xt|ut,xt-1) = N( At*miu_t-1 + Bt*ut, Rt) 根据连续系统的贝叶斯滤波公式： BEL(xn) = K*p(yt|xt) * ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1) 抛开前者的更新部分，使用后者的预测部分，来预测均值： BEL(xn) = ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1) 由于卡尔曼滤波的基本假设就是把贝叶斯滤波的BEL（x）假设为高斯分布，所以： *** BEL(xt-1) = N(miu_t-1, Pt-1) 这个***，结合前面那个高斯分布的***： p(xt|ut,xt-1) = N( At*miu_t-1 + Bt*ut, Rt) 所以预测部分的： BEL(xt)_bar = ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1) 就是两个高斯分布***的卷积： BEL(xt)_bar = ∫[ N( At*miu_t-1 + Bt*ut, Rt) * N(miu_t-1, Pt-1) ]d(xt-1) 依然是高斯分布。 根据正态分布定义计算得，其这个高斯分布的参数为： miu_t_bar = At*miu_t-1 + Bt*ut xigema2_bar = At*Pt*At` + Rt 即： BEL(xt)_bar = N( At*miu_t-1 + Bt*ut, At*Pt*At` + Rt ) 由于是预测，是均值，有bar。 7.3 观测过程 根据卡尔曼滤波器中的观测方程： yt = Ht*xt + δt 所以p(yt|xt)这个条件概率部分是一些高斯分布的线性组合： *** p(yt|xt) = N(yt; Ht*xt, Qt) 这里多出的yt；是用来表示这个计算需要用到yt。 根据连续系统的贝叶斯滤波： BEL(xt) = K*p(yt|xt) * ∫[ p(xt|ut, xt-1)*BEL(xt-1) ]d(xt-1) 这里考虑观测过程，即根据新数据yt更新xt，而需要预测的xt-1： BEL(xt) = K*p(yt|xt) * BEL(xt)_bar 这也是俩高斯分布的乘依然是高斯分布只不过两个参数的形式复杂一些。 由7.2已经有： *** BEL(xt)_bar = N(xt; miu_t_bar, Pt_bar) 结合前步骤的： *** p(yt|xt) = N(yt; Ht*xt, Qt) 得到新高斯的两个参数： miu_t = ut_bar + Kt*(yt − Ht*miu_t_bar) xigema2 = (I - Kt*Ht)*Pt_bar 其中Kt==Pt_bar*Ht`* (Ht*Pt_bar*Ht`+Qt)^-1 即： BEL(xt) = N( ut_bar + Kt*(yt − Ht*miu_t_bar) , (I - Kt*Ht)*Pt_bar ) 由于是更新，确定值，所以没有bar。 8、 结束 6的算法， 来自7的推导。 过程噪声矩阵Rt和观测噪声矩阵Qt的影响及调节： 这两者实际上是相对的，表示更相信观测传感器还是更相信预测模型。 使用时一般先根据传感器例如激光雷达的手册确定R，然后再根据R确定Q。 如果更相信观测数据，往小处调Q；如果不放心观测传感器，往大了调Q。 这样Q越大表示越不相信观测系统状态越容易收敛，对观测数据的响应越慢。 REF： http://blog.csdn.net/heyijia0327/article/details/17487467