机器人姿态（13）：姿态控制（再续）
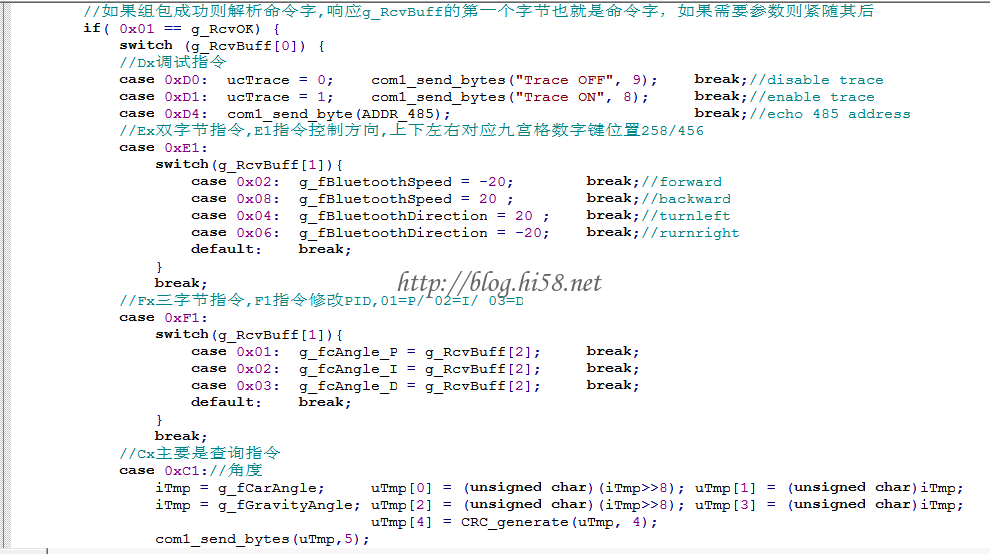
涉及的资源：中断0对左电机的旋转编码器计数，中断1对右电机编码器计数，定时器0产生20ms周期，串口1用于无线通讯。
使用中断较多，得合理分配优先级。
如果使用默认的，低优先级的这个串口中断会丢数据。
- PID设置
- 效果
这个调的算是差不多：
这个振荡的厉害：
按月份存档： 四月, 2016
机器人姿态（11）：姿态控制（续）
控制理论主要有经典控制、现代控制、智能控制三类。经典控制里面常用的有并联控制、串联控制两类。串联控制里面常用的是PID控制。
对于PID控制器，其传递函数为：
时域形式是
时域的另一种形式是使用时间常数
分析控制器的传递函数
可见极点位于原点，两个零点位于左平面，改变PID的三个参数可以改变零极点的位置。
按照自控原理，如果控制对象的响应稳定不受其它环节的影响，可以采用开环控制；反之如果被控对象受设定值、负载或者源端的影响而波动，应该选用闭环控制；闭环控制中常用的算法由比例、积分和微分三个部分组成，实际应用中通常只使用到其中的一项或两项，如P、PI、PD等。
- PID
所谓比例增益，积分增益，是PID控制的参数。比例控制是最常用的控制手段之一，也是最符合人的感观的一种控制。例如控制一个加热器，设定目标温度为100度；那么当开始加热时反馈温度离设定温度相差很远，这时电流很大；当温度接近设定值100度时，则电流很小；当温度达到设定值100度时，则电流关闭。
对于滞后性不是很大的控制对象，使用比例控制方式就可以满足控制要求。
比例常与积分一起进行控制，构成PI控制，u(t) = Kp*e(t) + Ki∑e(t) +u0。积分项是一个历史误差的累积值，如果光用比例控制时要不就是达不到设定值要不就是振荡，在使用了积分项后就可以解决达不到设定值的静态误差问题。
因为PI系统中的Ki的存在会使整个控制系统的响应速度受到影响，为了解决这个问题，可在控制中增加微分项D，微分项主要用来解决系统的响应速度问题，u(t) = Kp*e(t) + Ki∑e(t) + Kd[e(t) – e(t-1)]+u0。
- 伺服系统
众所周知伺服由3个反馈系统构成：位置环、速度环、电流环，根据使用的不同模式：力矩控制只需要调节电流环，速度控制需要调节电流环和速度环，位置控制需要调节电流环、速度环和位置环。越是内侧的环，越需要提高其响应性，不遵守这个原则，就会产生偏差和震动。
一般的，电流环为PI控制，速度环为PI控制以及力矩前馈控制，位置环为P控制以及速度前馈控制。电流环由于是最内侧的环，电机已确保其充分的响应性，所以一般只需要调整位置环和速度环。主要调整参数有三个：位置环的比例增益Kp、速度环的增益Kv和速度环积分时间常数I。
调整过程中，速度环的调整是整个系统调整中最关键的，也是最难调整的。但需要注意的是，在位置控制方式下，位置环增益和速度环参数有一定关联，当位置环增益提高对系统精度没有效果后，就需要再考虑提高速度环增益。
- 参数整定
实凑法：
首先，设控制器积分系数I为0，微分系数D为0；控制系统投入闭环运行，由小到大改变比例系数K，让扰动信号作阶跃变化，观察控制过程，直到获得满意的控制过程为止。
其次，然后取比例系数P为当前值乘以某个经验值例如0.83，由小到大增加积分系数I，同样让扰动信号作阶跃变化，直至求得满意的控制过程。再积分系数I保持不变，改变比例系数P，观察控制过程有无改善，如有改善则继续调整，直到满意为止。否则，将原比例系数P增大一些，再调整积分系数I力求改善控制过程。如此反复试凑，直到找到满意的比例系数P和积分系数I。
最后，引入适当的微分系数D，此时可适当增大比例系数P和积分系数I。和前述步骤相同，微分系数的整定也需反复调整，直到控制过程满意为止。
经验法：
理想曲线两个波，前高后低四一剖；一看二调多分析，调节质量不会低。
参数整定找最佳，从小到大顺序查；先是比例后积分，最后再把微分加。
曲线振荡很频繁，比例度盘要放大；曲线漂浮绕大湾，比例度盘往小扳。
曲线偏离回复慢，积分时间往下降；曲线波动周期长，积分时间再加长。
曲线振荡频率快，先把微分降下来；动差大来波动慢。微分时间应加长。
振荡法：
首先，只采用比例控制，使Kp从0增加到临界值Kr，这个临界值是指系统首次出现持续振荡时的增益值（如果不论怎样调整Kp都不会出现持续振荡，则振荡法不能用），出现持续振荡后测出振荡周期Pr。然后，齐格勒-尼柯尔斯提出可以根据下表中的公式确定Kp、Ti、Td。
- 作用
单独的P（比例）就是将差值进行成比例的运算，它的显著特点就是有差调节，有差的意义就是调节过程结束后，被调量不可能与设定值准确相等，它们之间一定有残差，残差具体值可以通过比例关系计算出。增加比例将会有效减小残差并增加系统响应，但容易导致系统激烈震荡甚至不稳定。
单独的I（积分）就是使调节器的输出信号的变化速度与差值信号成正比，如果差值大，则积分环节的变化速度大，这个环节的正比常数的比例倒数在伺服系统里通常叫为积分时间常数，积分时间常数越小意味着系统的变化速度越快，所以同样如果增大积分速度（也就是减小积分时间常数）将会降低控制系统的稳定程度，直到最后出现发散的震荡过程。这个环节最大的好处就是被调量最后是没有残差的。
单独的D（微分）就是根据差值的方向和大小进行调节的，调节器的输出与差值对于时间的导数成正比，微分环节只能起到辅助的调节作用，它可以与其他调节结合成PD和PID调节。它的好处是可以根据被调节量（差值）的变化速度来进行调节，而不要等到出现了很大的偏差后才开始动作，其实就是赋予了调节器以某种程度上的预见性，可以增加系统对微小变化的响应特性。
机器人姿态（09）：姿态控制
- 一般模型
现实世界常见的是一阶惯性系统和二阶震荡系统，后者最常见的例如R-L-C电路系统和M-b-k机械系统，对于后者：
根据力学牛顿方程，有以下常系数现行微分方程成立：
以力F为输入以位移x为输出，传递函数为：
加上控制器Gc之后，系统框图为：
如果Gc(s)是PID控制器，框图为：
上图中校正装置的传递函数为：
假设，车体质量M=1Kg，阻尼b=2N/m.s^-1，弹簧刚度k=25N/m，F=1N，b/2sqrt(km)=2/2sqrt(1*25)=0.2，是个欠阻尼系统，讨论如下。
比例控制
可见，比例控制可以提高开环增益而且不影响相位，能够减少稳态误差但是不能最终消除，Kp越大超调越大响应越快系统越不稳定。
比例积分控制
可见，PI调节相位裕度会下降，稳定性会变差，积分时间常数Ti越小超调越大响应越快，几分环节对于有差系统时需要的。
比例微分控制
微分调节对于输出量的变化和波动产生强烈的阻尼和抑制作用，就像摩擦力一样，从而使得输出平稳。所以微分控制对于无变化或变化缓慢的对象不起作用。微分控制量正比于输出与输入的差的变化率，变化越剧烈调节作用越明显，变化越平稳调节作用越弱。所以微分环节对于具有较大惯性或滞后的被控对象时需要的，可以改善动态特性；但是同时也放大了高频噪声，高频抗干扰能力会减弱。仿真图中，微分Td越大超调减小响应加快。
比例积分微分控制
PID全用，最好使得积分作用于低频段以提高稳定性，微分发生在高频段以改进动态性能。缺点是三个参数都需要整定。
- 简化模型
实际上汽车可以忽略弹簧k从而简化为质量–阻尼系统，而且更关注的是速度响应，而不是距离位移，假设小车质量m=1.5Kg，摩擦系数b=2N/m.s^-1，电机牵引力F=1N：
对牛顿方程F-bv=Ma，进行拉斯变换之后为：
可见该小车为一阶惯性系统，负载质量m相当于该惯性环节的时间常数，通过施加闭环调整环节，可以减少该时间常数，从而相当于减轻质量，最终便于控制。
比例控制
比例积分控制
比例积分微分控制
机器人姿态（07）：姿态获取（续）
从类似小米平衡车里面的MPU，可以计算得到几个不同的小车倾角，分别是根据加速度计算出的倾角、根据陀螺仪计算出的倾角和互补算法计算出的倾角、卡尔曼算法计算出的倾角。
-
加速度计算的角度
加速度计可以测量某时刻XYZ三个方向的加速度值，而通过重力加速度在XYZ三个轴的分量，就可以计算出小车的倾角。
不过小车在非静止状态下，加速度计测得的结果并不非常精确。因为小车在动态时受电机作用还有前进或者后退的力，所以加速度计测得是总的加速度。这表明加速度数据在静态下才准确，不过好消息是陀螺仪在动态下的数据准确，所以需要综合加速度计的加速度数据和陀螺仪的角速度数据才会更准确，这些是所谓的互补算法或卡尔曼滤波算法。
从简单的开始，把MPU平放在车体上，定义X为前进方向，则Y轴平行于左右车轮的轴线，如下图：
可见车体Y轴与地平面夹角是不会发生变化的，一直为0度。能发生变化的是X轴与平面的夹角，或者说Z轴与平面的夹角，可以证明X轴Z轴夹角变化是一致的。下面抛开上面的透视图，采用正试图来看：
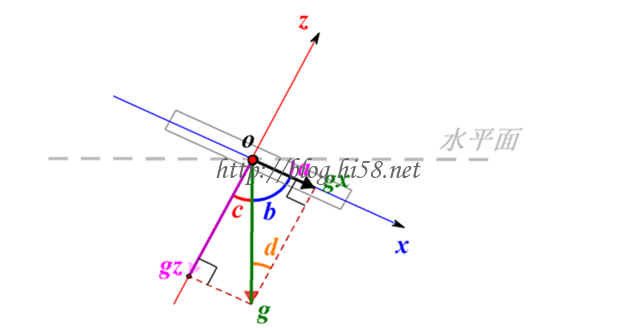
上图中，g为重力加速度，gx和gz为MPU测得的加速度数据，但同时也是重力加速度在x和z轴的分量。
很容易看出小车倾角就是atan（gx/gz），实际使用考虑到零点偏移：Angle_Z = (AccZ – AccZ_Offset) * R_Z。
其中AccZ是Z轴加速度实时测得的数据，AccZ_Offset是Z轴加速度的静差，R_Z是加速度计Z轴比例系数。
上面是用的三角函数的反正切函数，从数值计算角度也可以用asin（gx/g），因为在小角度时候有sin（dalpha）=alpha的近似（弧度方式）成立。角度方式是sin（alpha）=alpha*pi/180，MPU给出的是后面这种角度方式。经过拟合试验后可以进一步作修正：sin（alpha）=0.92*alpha*pi/180，因此由gx/g=sin(alpha)=0.92*alpha*pi/180，可以得角度alpha=180*gx/0.92*pi*g，这是个近似的方法，这个数据不很准确，单是速度快。
- 陀螺仪计算的角度
通过陀螺仪计算角度很简单，陀螺仪测得的是角速度，角速度乘某段时间就是该段时间所转过的角度，如果再把每次计算所得的角度累加（积分）就得到当前位置的倾角了。
假设，陀螺仪是最初平行于桌面，单片机每delta_t时间读一次陀螺仪的角速度，读三次以后 Z轴顺时针转到下图中位置：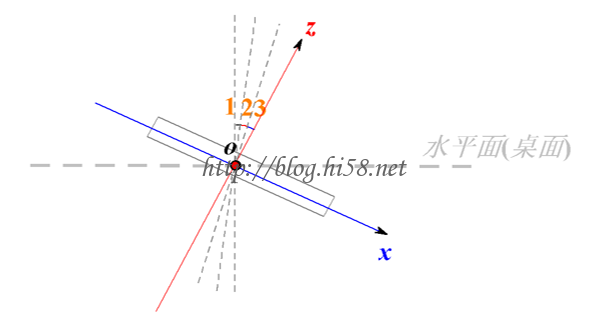
那么这段时间内转过的总角度为角1+角2+角3，如果陀螺仪测得的角速度分别为w1/w2/w3，则总角度为w1*delt_t1+w2*delta_t2+w3*delta_t3，这其实就是个离散积分的过程，一般写成：angle_n = angle_n-1 + (Gyro – Gyro_Offset) * R_Gyro。
其中angle_n是当前角度值，angle_n-1是上次计算所得的角度。Gyro是陀螺仪实时测得角速度，Gyro_Offset是陀螺仪零点偏移值。R_Gyro是陀螺仪比例。
但陀螺仪计算所得的角度也存在误差，而且误差越积累越大，最终导致计算角度与实际角度相差很大，因此需要考虑加速度计算的角度。
- 互补算法计算的角度
//一阶互补算法
factor = 0.095;
K =factor / (factor + delta_t); //K开始时0.98
angle_Comp1 = K * (angle_Comp1 + omega * delta_t) + (1-K) * angle_Acc;
// 二阶互补算法
factor = 0.2;
x1 = (angle_Acc – angle_Comp2)*(1-factor)*(1-factor);
y1 = y1 + x1 * delta_t;
x2 = y1 + 2 * (1-factor) *(angle_Acc – angle_Comp2) + omega;
angle_Comp2 = angle_Comp2 + x2 * delta_t;
- 卡尔曼算法计算的角度
angle_Kalman += (omega – Gbias) * delta_t; //先验估计
Pdot[0] = -PP[0][1] – PP[1][0] + Q_angle;
Pdot[1] = – PP[1][1];
Pdot[2] = – PP[1][1];
Pdot[3] = Q_gbias;//PP[0][0] += Pdot[0] * delta_t;
PP[0][1] += Pdot[1] * delta_t;
PP[1][0] += Pdot[2] * delta_t;
PP[1][1] += Pdot[3] * delta_t; //先验估计误差协方差PCt_0 = C_0 * PP[0][0]; PCt_1 = C_0 * PP[1][0];
E = R_angle + C_0 * PCt_0;if(E!=0) {
K_0 = PCt_0 / E; K_1 = PCt_1 / E;
}PP[0][0] -= K_0 * PCt_0;
PP[0][1] -= K_0 * PCt_1;
PP[1][0] -= K_1 * PCt_0;
PP[1][1] -= K_1 * PCt_1; //后验估计协方差angle_Err = angle_Acc – angle_Kalman;
angle_Kalman += K_0 * angle_Err; //后验估计
Gbias += K_1 * angle_Err;
rris
rris